题目内容
5.已知a=$\sqrt{2}$,则($\frac{1}{a+1}$-$\frac{a-2}{{a}^{2}+a}$)÷$\frac{1}{a+1}$的值是$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=$\frac{a-a+2}{a(a+1)}$•(a+1)
=$\frac{2}{a(a+1)}$•(a+1)
=$\frac{2}{a}$,
当a=$\sqrt{2}$时,原式=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.冬季某天我国三个城市的最高气温分别是-11℃,3℃,-3℃,它们任意两城市中最大的温差是( )
| A. | 11℃ | B. | 13℃ | C. | 14℃ | D. | 6℃ |
13.已知P、Q是线段AB的两个黄金分割点,且AB=10,则PQ长为( )
| A. | $5\sqrt{5}-5$ | B. | $5\sqrt{5}+1$ | C. | 10$\sqrt{5}$-20 | D. | $15-5\sqrt{5}$ |
17.下列说法正确的是( )
| A. | 任何数都有两个平方根 | B. | 若a2=b2,则a=b | ||
| C. | $\sqrt{4}$=±2 | D. | -8的立方根是-2 |
14.若分式$\frac{{x}^{2}-4}{x-2}$的值为0,则x的取值为( )
| A. | x=2 | B. | x=-2 | C. | x=2 | D. | 无法确定 |
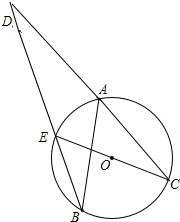 如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.
如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.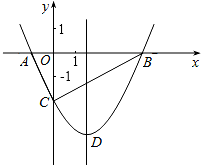 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).