题目内容
8．下列长度的三条线段能构成三角形的是（ ）| A． | 4，5，10 | B． | 2，6，8 | C． | 3，4，5 | D． | 5，7，13 |
分析 根据三角形的三边关系进行分析判断．
解答 解：根据三角形任意两边的和大于第三边，得
A中，5+4=9＜10，不能组成三角形；
B中，2+6=8，不能组成三角形；
C中，3+4=7＞5，能够组成三角形；
D中，5+7=12＜13，不能组成三角形．
故选C．
点评 本题考查了能够组成三角形三边的条件：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．
练习册系列答案
相关题目
18．
有这样一个问题：探究函数y=x-$\frac{2}{x}$的图象和性质．
小石根据学习函数的经验，对此函数的图象和性质进行了探究．
下面是小石的探究过程，请补充完整：
（1）函数的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
求m的值；
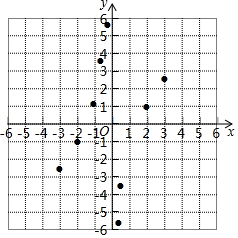
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出此函数的图象；
（4）进一步探究，结合函数的图象，写出此函数的性质（一条即可）：当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而增大．
有这样一个问题：探究函数y=x-$\frac{2}{x}$的图象和性质．小石根据学习函数的经验，对此函数的图象和性质进行了探究．
下面是小石的探究过程，请补充完整：
（1）函数的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{7}{3}$ | -1 | 1 | $\frac{7}{2}$ | $\frac{17}{3}$ | -$\frac{17}{3}$ | -$\frac{7}{2}$ | m | 1 | $\frac{7}{3}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出此函数的图象；
（4）进一步探究，结合函数的图象，写出此函数的性质（一条即可）：当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而增大．
19．在△ABC中，AB=AC，如果AB边上的高等于AB的一半，那么∠A的度数为（ ）
| A． | 150° | B． | 150°和45° | C． | 30° | D． | 150°和30° |
16．如果xa-b-2ya+b-4=10是二元一次方程，那么a、b的值分别是（ ）
| A． | 3、1 | B． | 3、2 | C． | 2、1 | D． | 2、-1 |
3．下列各式：$\frac{2}{x}$、$\frac{x+2}{2}$、$\frac{x-xy}{x}$、3x+$\frac{y}{3}$、$\frac{3x}{π+2}$、$\frac{3{x}^{2}-4}{0.5}$中，分式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
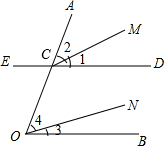如图，ED，CM与AO交于C点，OB，ON与AO交于O点，那么下列说法正确的是（ ）