题目内容
13.在正方形ABCD中,点E,F分别在线段BC,CD上,且∠BAE=20°,∠DAF=25°,则∠CEF=40°.分析 延长EB至G,使BG=DF,连接AG.利用正方形的性质,证明ABG≌△ADF,△FAE≌△GAE,
解答 解:延长EB至G,使BG=DF,连接AG,
∵正方形ABCD,
∴AB=AD,∠ABG=∠ADF=∠BAD=90°,
∵BG=DF,
∴△ABG≌△ADF,
∴AG=AF,
∵∠BAE=20°,∠DAF=25°,
∴∠FAE=∠GAE=45°,
∵AE=AE,
∴△FAE≌△GAE,
∴∠AEB=∠AEF=70°,
∴∠CEF=180°-∠AEB-∠AEF=40°,
故答案为40°
点评 本题考查了正方形的性质、全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.直线y=(3-π)x经过的象限是( )
| A. | 一、二象限 | B. | 一、三象限 | C. | 二、三象限 | D. | 二、四象限 |
8.下列长度的三条线段能构成三角形的是( )
| A. | 4,5,10 | B. | 2,6,8 | C. | 3,4,5 | D. | 5,7,13 |
5. 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )
 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )| A. | 70° | B. | 110° | C. | 120° | D. | 60° |
2.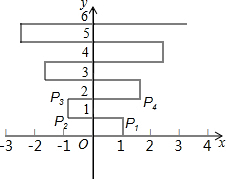 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
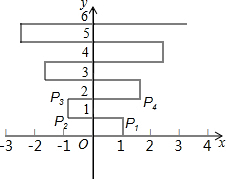 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )| A. | (504,1007) | B. | (505,1009) | C. | (1008,1007) | D. | (1009,1009) |
3.已知$\left\{\begin{array}{l}{a+2b=4}\\{3a+2b=8}\end{array}\right.$,则2a+2b等于( )
| A. | 6 | B. | $\frac{16}{3}$ | C. | 4 | D. | 2 |
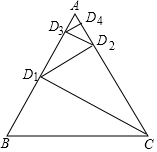 某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a.
某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a.