题目内容
3.下列各式:$\frac{2}{x}$、$\frac{x+2}{2}$、$\frac{x-xy}{x}$、3x+$\frac{y}{3}$、$\frac{3x}{π+2}$、$\frac{3{x}^{2}-4}{0.5}$中,分式有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据分式的定义,可得答案.
解答 解:$\frac{2}{x}$,$\frac{x-xy}{x}$是分式,有2个,
故选B.
点评 本题考查了分式的定义,分母中含有字母的式子是分式.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
14. 如图,在△ABC中,∠B=70°,D为BC上的一点,若∠ADC=2x,则x的度数可能为( )
如图,在△ABC中,∠B=70°,D为BC上的一点,若∠ADC=2x,则x的度数可能为( )
 如图,在△ABC中,∠B=70°,D为BC上的一点,若∠ADC=2x,则x的度数可能为( )
如图,在△ABC中,∠B=70°,D为BC上的一点,若∠ADC=2x,则x的度数可能为( )| A. | 30 | B. | 60 | C. | 90 | D. | 100 |
8.下列长度的三条线段能构成三角形的是( )
| A. | 4,5,10 | B. | 2,6,8 | C. | 3,4,5 | D. | 5,7,13 |
15.下列计算正确的是( )
| A. | a3•a2=a6 | B. | a3-a2=a | C. | (-a3)2=a6 | D. | a6÷a2=a3 |
12.分式方程$\frac{x}{x+2}$=$\frac{1}{2}$的解是( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
13.阅读下列材料:
某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
m的值为50;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式y=15x+20;
当4<x≤16时,写出一个符合表中数据的函数解析式$\frac{320}{x}$;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源56min.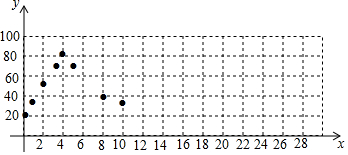
某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
| 接通电源后的时间x (单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
| 水箱中水的温度y (单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式y=15x+20;
当4<x≤16时,写出一个符合表中数据的函数解析式$\frac{320}{x}$;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源56min.


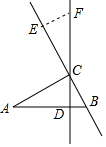 如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.