题目内容
18. 有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.
有这样一个问题:探究函数y=x-$\frac{2}{x}$的图象和性质.小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{7}{3}$ | -1 | 1 | $\frac{7}{2}$ | $\frac{17}{3}$ | -$\frac{17}{3}$ | -$\frac{7}{2}$ | m | 1 | $\frac{7}{3}$ | … |
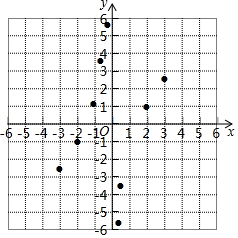
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可):当x<0时,y随x的增大而增大;当x>0时,y随x的增大而增大.
分析 (1)分母不等于0即可得;
(2)将x=1代入解析式即可得m的值;
(3)将各点分y轴左右两侧,按自变量总小到大用平滑曲线依次连接可得;
(4)结合图象可从函数的增减性、与y轴交点情况及对称性解答均可.
解答 解:(1)函数y=x-$\frac{2}{x}$的自变量x的取值范围是x≠0,
故答案为:x≠0.
(2)当x=1时,y=1-2=-1,即m=-1.
(3)此函数的图象如右图所示.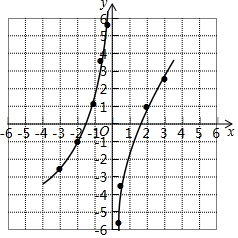
(4)此函数的性质:
①当x<0时,y随x的增大而增大;当x>0时,y随x的增大而增大.
②关于原点成中心对称.
③函数的图象与y轴无交点.
故答案为:当x<0时,y随x的增大而增大;当x>0时,y随x的增大而增大(一条即可).
点评 本题主要考查反比例函数的图象和性质,会用描点法画出函数图象,利用数形结合的思想写出函数的性质是解题的关键.

练习册系列答案
相关题目
8.下列长度的三条线段能构成三角形的是( )
| A. | 4,5,10 | B. | 2,6,8 | C. | 3,4,5 | D. | 5,7,13 |
 如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC=1m,
如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC=1m,
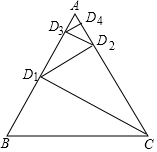 某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a.
某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a.