题目内容
15.解分式方程:$\frac{2}{x+3}$+$\frac{1}{3-x}$=$\frac{1}{{x}^{2}-9}$.分析 根据等式的性质,可化为整式方程,根据解整式方程,可得答案.
解答 解:两边都乘以(x+3)(x-3),得
2(x-3)-(x+3)=-1,
解得x=10,
检验:当x=10时,x2-9≠0
∴原方程的解为x=10.
点评 本题考查了解分式方程,利用等式的性质得出整式方程是解题关键,要检验分式方程的根.

练习册系列答案
相关题目
10. 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )
 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,AD=1,则BD的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
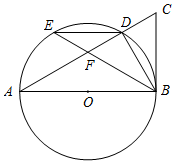 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.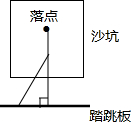 如图,体育课上老师测量跳远成绩是这样操作的:用一块直角三角板的一边附在踏跳板上,另一边与拉直的皮尺重合,并且使皮尺经过被测试同学的落点,这样做的理由是垂线段最短.
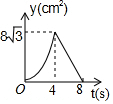
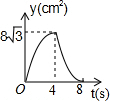
如图,体育课上老师测量跳远成绩是这样操作的:用一块直角三角板的一边附在踏跳板上,另一边与拉直的皮尺重合,并且使皮尺经过被测试同学的落点,这样做的理由是垂线段最短.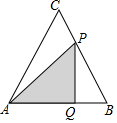 如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )
如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )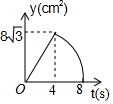
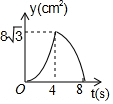
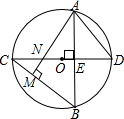 如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.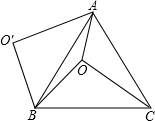 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,则∠AOB=150°.
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,则∠AOB=150°.