题目内容
20.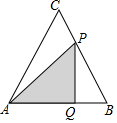 如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )
如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )| A. | 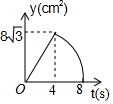 | B. | 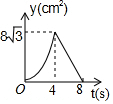 | C. | 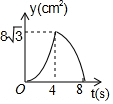 | D. | 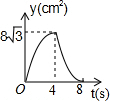 |
分析 分为两种情况,P在A上和P在BC上,根据等边三角形的性质求出∠A=∠B=60°,解直角三角形求出AQ、PQ,根据面积公式求出面积y,根据函数的解析式得出即可.
解答 解:
分为两种情况:①当P在AC上时,如图1,
∵△ABC是等边三角形,
∴∠A=60°,
∵PQ⊥AB,
∴∠PQA=90°,
∴∠APQ=30°,
∵AP=2x,
∴AQ=x,PQ=$\sqrt{3}$x,
∴y=$\frac{1}{2}×AQ×PQ$=$\frac{1}{2}•x•\sqrt{3}x$=$\frac{1}{2}\sqrt{3}$x2,
此时函数的图象是顶点在原点上,开口向上的抛物线,∴选项A、D错误;
②当P在BC上时,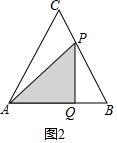
此时AC+CP=2x,
BP=8+8-2x=16-2x,
∠B=60°,
BQ=$\frac{1}{2}$BP=8-x,PQ=$\sqrt{3}$BQ=$\sqrt{3}$(8-x),
所以y=$\frac{1}{2}$AQ×PQ=$\frac{1}{2}$×[8-(8-x)]×$\sqrt{3}$(8-x)=-$\frac{\sqrt{3}}{2}$(x-4)2+8$\sqrt{3}$,
所以此时函数的图象的顶点坐标是(4,8$\sqrt{3}$),开口方向向下的抛物线,∴选项C正确,选项B错误;
故选C.
点评 本题考查了动点问题的函数图象问题、函数的图象和性质等知识点,能求出符合的函数的解析式是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.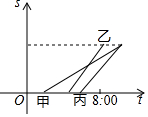 甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
 甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 甲车和乙车 |
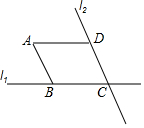 如图,直线l1与直线l2相交于点C,点B,D分别在l1,l2上,且BC=CD=3,分别过点B,D作l2,l1的平行线相交于点A.若点A到直线l1的距离为2,则点A到直线l2的距离为2.
如图,直线l1与直线l2相交于点C,点B,D分别在l1,l2上,且BC=CD=3,分别过点B,D作l2,l1的平行线相交于点A.若点A到直线l1的距离为2,则点A到直线l2的距离为2. 已知,如图,在△ABC中,∠A=55°,∠B=95°,将纸片的一角折叠,使点C落在△ABC外.若∠2=25°,则∠1的度数为85°.
已知,如图,在△ABC中,∠A=55°,∠B=95°,将纸片的一角折叠,使点C落在△ABC外.若∠2=25°,则∠1的度数为85°.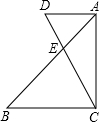 将一副三角板按如图所示的方式摆放,其中∠CAD=∠ACB=90°,∠ACD=30°,∠B=45°,则有下列结论:①AD:BC=AE:CE;②∠BEC=70°;③BC=$\sqrt{3}$AD;④CD:AB=2:$\sqrt{6}$,其中正确结论的序号是③④.(把所有正确结论的序号都填在横线上)
将一副三角板按如图所示的方式摆放,其中∠CAD=∠ACB=90°,∠ACD=30°,∠B=45°,则有下列结论:①AD:BC=AE:CE;②∠BEC=70°;③BC=$\sqrt{3}$AD;④CD:AB=2:$\sqrt{6}$,其中正确结论的序号是③④.(把所有正确结论的序号都填在横线上) 如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC.
如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC.