题目内容
20.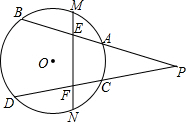 点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.
点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.
分析 首先连接AM,CN,根据圆心角、弧、弦之间的关系和圆周角定理得出∠MAE和∠EMA的度数和等于$\widehat{BM}$、$\widehat{AC}$、$\widehat{CN}$度数和的一半,∠FCN和∠CNF的度数和等于$\widehat{DN}$、$\widehat{AC}$、$\widehat{AM}$度数和的一半,继而可证得∠MAE+∠EMA=∠FCN+∠CNF,则可得∠PEF=∠PFE,然后证得PE=PF,
解答 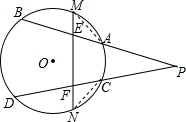 解:证明:连接AM和CN,
解:证明:连接AM和CN,
∵点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,
∴$\widehat{BM}$=$\widehat{AM}$,$\widehat{DN}$=$\widehat{CN}$,
∵∠MAE和∠EMA的度数和等于$\widehat{BM}$、$\widehat{AC}$、$\widehat{CN}$度数和的一半,
∠FCN和∠CNF的度数和等于$\widehat{DN}$、$\widehat{AC}$、$\widehat{AM}$度数和的一半,
∴∠MAE+∠EMA=∠FCN+∠CNF,
∵∠PEF=∠MAE+∠EMA,∠PFE=∠FCN+∠CNF,
∴∠PEF=∠PFE,
∴PE=PF,
即△PEF是等腰三角形.
点评 此题考查了圆周角定理以及等腰三角形的判定.注意作出辅助线,掌握圆周角与弧的关系是关键.

练习册系列答案
相关题目
8.若三角形三边a、b、c满足$\frac{1}{a}$-$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a-b+c}$,则这个三角形一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 正三角形 | D. | 等腰直角三角形 |
15.若(a2+b2-1)2=16,则a2+b2的值为( )
| A. | 5 | B. | -3 | C. | -3或5 | D. | -7或9 |
5. 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )
 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )| A. | AB⊥BC | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
9.某林业部门要查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
所以可以估计这种幼树移植成活的概率为( )
| 移植总数(n) | 成活数(m) | 成活的频率($\frac{m}{n}$) |
| 10 | 8 | 0.80 |
| 50 | 47 | 0.94 |
| 270 | 235 | 0.870 |
| 400 | 369 | 0.923 |
| 750 | 662 | 0.883 |
| 1500 | 1335 | 0.89 |
| 3500 | 3203 | 0.915 |
| 7000 | 6335 | 0.905 |
| 9000 | 8073 | 0.897 |
| 14000 | 12628 | 0.902 |
| A. | 0.1 | B. | 0.2 | C. | 0.8 | D. | 0.9 |