题目内容
10.①计算:$\sqrt{27}-\frac{1}{2cos30°}+\sqrt{1\frac{1}{3}}$②用配方法解方程:x2+2x-5=0.
分析 ①先把各二次根式化为最简二次根式,然后合并即可;
②利用配方法得到(x+1)2=6,然后利用直接开平方法解方程.
解答 解:①原式=3$\sqrt{3}$-$\frac{1}{2×\frac{\sqrt{3}}{2}}$+$\frac{2\sqrt{3}}{3}$
=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$
=$\frac{10\sqrt{3}}{3}$;
②x2+2x=5,
x2+2x+1=6,
(x+1)2=6,
x+1=±$\sqrt{6}$,
所以x1=-1+$\sqrt{6}$,x2=-1-$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了特殊角的三角函数值和配方法解一元二次方程.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
20.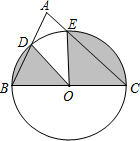 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )| A. | $\frac{7}{18}π$ | B. | $\frac{7}{9}π$ | C. | $\frac{14}{9}π$ | D. | $\frac{28}{9}π$ |
1.若a<b,则下列各式中一定成立的是( )
| A. | a+2>b+2 | B. | a-2>b-2 | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
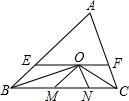 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC分别于点E,F,作OM∥AB,ON∥AC,交BC分别于M,N.若AB=10,AC=8,BC=9,
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC分别于点E,F,作OM∥AB,ON∥AC,交BC分别于M,N.若AB=10,AC=8,BC=9, 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.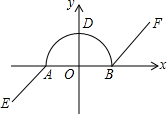 如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.
如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.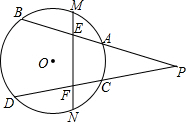 点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.
点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.