题目内容
8.若三角形三边a、b、c满足$\frac{1}{a}$-$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a-b+c}$,则这个三角形一定是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 正三角形 | D. | 等腰直角三角形 |
分析 满足$\frac{1}{a}$-$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a-b+c}$,进行化简,然后再进行整理即可得出结果.
解答 解:∵$\frac{1}{a}$-$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a-b+c}$,
∴bc(a+b-c)+ac(a+b-c)-ab(a+b-c)=abc,
即abc+b2c-bc2+a2c+abc-ac2-a2b-ab2+abc-abc=0,
合并得:b2c-bc2+a2c-ac2-a2b-ab2+2abc=0,
(a2b-a2c)+(-abc+ac2)+(ab2-abc)+(-b2c+bc2)=0,
a2(b-c)-ac(b-c)+ab(b-c)-bc(b-c)=0,
(a2-ac+ab-bc)(b-c)=0,
[a(a-c)+b(a-c)](b-c)=0,
∴(a+b)(a-c)(b-c)=0,
∴a=c或b=c,
∴这个三角形一定是等腰三角形.
故选:A.
点评 本题主要考查了分式的混合运算,在解题时要注意利用已知条件,把分式变为整式,进一步分组分解因式求得a、b、c的关系解决问题.

练习册系列答案
相关题目
17.因式分解3y2-6y+3,结果正确的是( )
| A. | 3(y-1)2 | B. | 3(y2-2y+1) | C. | (3y-3)2 | D. | $\sqrt{3}(y-1)^{2}$ |
18.-3的绝对值等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | $\sqrt{3}$ |
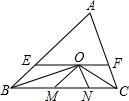 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC分别于点E,F,作OM∥AB,ON∥AC,交BC分别于M,N.若AB=10,AC=8,BC=9,
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC分别于点E,F,作OM∥AB,ON∥AC,交BC分别于M,N.若AB=10,AC=8,BC=9, 如图,四边形ABCD是矩形:
如图,四边形ABCD是矩形: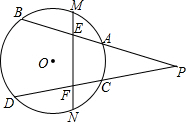 点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.
点P是圆外一点,点M,N分别是弧$\widehat{AB}$、$\widehat{CD}$的中点,求证:△PEF为等腰三角形.