题目内容
18.已知三点(-4,y1),(1,y2),(5,y3)均在抛物线y=-2ax2+4ax+3(a<0)上,则下列关系正确的是( )| A. | y1<y3<y2 | B. | y3<y2<y1 | C. | y2<y3<y1 | D. | y1<y2<y3 |
分析 求得抛物线对称轴为直线x=1,根据抛物线的性质,抛物线上的点离对称轴越远,对应的函数值就越大,由x取1、5、-4时,x取-4时所对应的点离对称轴最远,x取1时所对应的点是顶点,在对称轴上,即可得到答案.
解答 解:∵抛物线y=-2ax2+4ax+3(a<0),
∴-2a>0,
∴抛物线的开口向上,对称轴是直线x=-$\frac{4a}{2×(-2a)}$=1,
∴抛物线上的点离对称轴越远,对应的函数值就越大,
∵x取-4时所对应的点离对称轴最远,x取1时所对应的点是顶点,
∴y2<y3<y1.
故选C.
点评 本题考查了二次函数图象上点的坐标特征.解题时,需熟悉抛物线的有关性质:抛物线的开口向上,则抛物线上的点离对称轴越远,对应的函数值就越大.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.某营业厅对手机话费业务有如下的优惠;
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每月末的话费余额是y(元),月数为x(个),则:
(1)每个月等额返还的话费是25元,第2个月末的话费余额是112元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
| 优惠规则: ①用户手机原有话费不能低于240元; ②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费, ③后将这300元话费分12次,在每月的15号等额返还到手机账户; ④每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用; 每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额话费. |
(1)每个月等额返还的话费是25元,第2个月末的话费余额是112元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
13.下列说法正确的是( )
| A. | 不可能事件发生的概率为0 | |
| B. | 随机事件发生的概率为$\frac{1}{2}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次 |
3. 如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为( )
如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为( )
 如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为( )
如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
8.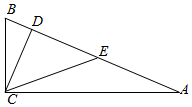 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )| A. | 2a | B. | 2$\sqrt{2}$a | C. | 3a | D. | $\frac{4\sqrt{3}}{3}a$ |
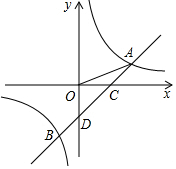 如图,一次函数y=ax-1的图象与反比例函数y=$\frac{k}{x}$的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
如图,一次函数y=ax-1的图象与反比例函数y=$\frac{k}{x}$的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.