题目内容
6.某营业厅对手机话费业务有如下的优惠;| 优惠规则: ①用户手机原有话费不能低于240元; ②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费, ③后将这300元话费分12次,在每月的15号等额返还到手机账户; ④每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用; 每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额话费. |
(1)每个月等额返还的话费是25元,第2个月末的话费余额是112元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
分析 (1)根据每月返还钱数=总钱数÷12,即可求出每个月等额返还的话费,再用总钱数-240-2个月的月初扣费+2个月的月中返还,即可求出第2个月末的话费余额;
(2)根据每月末的话费余额=总钱数-240-每月初扣费×月数+每月中返还×月数,即可得出y与x之间的函数关系式;
(3)令y=-24x+160<49,解之即可得出x的取值范围,取其内的最小正整数即可得出结论.
解答 解:(1)300÷12=25(元),
400-240-49×2+25×2=112(元).
故答案为:25;112.
(2)根据题意得:y=400-240-49x+25x=-24x+160.
(3)令y=-24x+160<49,
解得:x>4$\frac{5}{8}$,
∵x为正整数,
∴x≥5,
∴第5个月底费用已不足49元,第6个月欠费.
答:若不续费,小明的手机第6个月会欠费.
点评 本题考查了一次函数的应用以及解一元一次不等式,解题的关键是:(1)根据数量关系,列式计算;(2)根据数量关系,列出y与x之间的函数关系式;(3)结合(2)找出关于x的一元一次不等式.

练习册系列答案
相关题目
17. 一次函数y=kx+b图象如图所示,则关于x的不等式kx+b<0的解集为( )
一次函数y=kx+b图象如图所示,则关于x的不等式kx+b<0的解集为( )
 一次函数y=kx+b图象如图所示,则关于x的不等式kx+b<0的解集为( )
一次函数y=kx+b图象如图所示,则关于x的不等式kx+b<0的解集为( )| A. | x<-5 | B. | x>-5 | C. | x≥-5 | D. | x≤-5 |
11.九一(1)班在参加学校4×100m接力赛时,安排了甲,乙,丙,丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
18.已知三点(-4,y1),(1,y2),(5,y3)均在抛物线y=-2ax2+4ax+3(a<0)上,则下列关系正确的是( )
| A. | y1<y3<y2 | B. | y3<y2<y1 | C. | y2<y3<y1 | D. | y1<y2<y3 |
15.已知等腰三角形的两边a,b的长是方程组$\left\{\begin{array}{l}{2x+y=10}\\{x+2y=8}\end{array}\right.$的解,则这个三角形的周长是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
16.若a+b=3,a2+b2=7,则ab等于( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
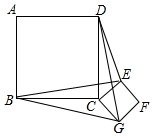 如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号)
如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号)