题目内容
8.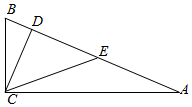 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )| A. | 2a | B. | 2$\sqrt{2}$a | C. | 3a | D. | $\frac{4\sqrt{3}}{3}a$ |
分析 根据勾股定理得到CE=$\sqrt{2}$a,根据直角三角形的性质即可得到结论.
解答 解:∵CD⊥AB,CD=DE=a,
∴CE=$\sqrt{2}$a,
∵在△ABC中,∠ACB=90°,点E是AB的中点,
∴AB=2CE=2$\sqrt{2}$a,
故选B.
点评 本题考查了直角三角形斜边上的中线,能求出AE=CE是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知三点(-4,y1),(1,y2),(5,y3)均在抛物线y=-2ax2+4ax+3(a<0)上,则下列关系正确的是( )
| A. | y1<y3<y2 | B. | y3<y2<y1 | C. | y2<y3<y1 | D. | y1<y2<y3 |
16.若a+b=3,a2+b2=7,则ab等于( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
3.计算$\frac{3x}{(x-1)^{2}}$-$\frac{3}{(x-1)^{2}}$的结果是( )
| A. | $\frac{x}{(x-1)^{2}}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{3}{x-1}$ | D. | $\frac{3}{x+1}$ |
20. 已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )
已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )
 已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )
已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )| A. | 100° | B. | 135° | C. | 155° | D. | 165° |
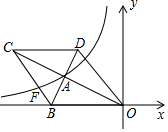 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32.
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32.