题目内容
在平面直角坐标系中,将二次函数y=3x2的图象向左平移2个单位,所得图象的解析式为( )
| A、y=3x2-2 |
| B、y=3x2+2 |
| C、y=3(x-2)2 |
| D、y=3(x+2)2 |
考点:二次函数图象与几何变换
专题:数形结合
分析:先确定抛物线y=3x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)向左平移2个单位所得对应点的坐标为(-2,0),然后利用顶点式写出新抛物线解析式即可.
解答:解:抛物线y=3x2的顶点坐标为(0,0),把点(0,0)向左平移2个单位所得对应点的坐标为(-2,0),所以平移后的抛物线解析式为y=3(x+2)2.
故选D.
故选D.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
在平面直角坐标系中,点(3,-5)关于x轴的对称点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
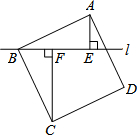 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
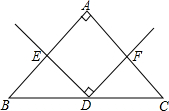 已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.
已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.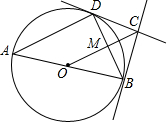 如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.
如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.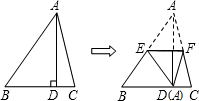 如图,在△ABC中,AB=12,AC=10,BC=9,AD⊥BC.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为
如图,在△ABC中,AB=12,AC=10,BC=9,AD⊥BC.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为 已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.
已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.