题目内容
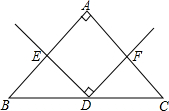 已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.
已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.考点:全等三角形的判定与性质
专题:证明题
分析:如图,作辅助线;证明△AED≌△CFD,即可解决问题.
解答: 解:如图,连接AD;
解:如图,连接AD;
∵∠A=90°,AB=AC,D是BC的中点,
∴AD=BD=CD,AD⊥BC,∠B=∠C=45°;
∴∠BAD=90°-45°=45°;
∵∠EDF=∠ADC=90°,
∴∠EDA=∠FDC;在△AED与△CFD中,
,
∴△AED≌△CFD(ASA),
∴DE=DF.
 解:如图,连接AD;
解:如图,连接AD;∵∠A=90°,AB=AC,D是BC的中点,
∴AD=BD=CD,AD⊥BC,∠B=∠C=45°;
∴∠BAD=90°-45°=45°;
∵∠EDF=∠ADC=90°,
∴∠EDA=∠FDC;在△AED与△CFD中,
|
∴△AED≌△CFD(ASA),
∴DE=DF.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用等边三角形的性质、全等三角形的判定等几何知识点来分析、判断.

练习册系列答案
相关题目
在平面直角坐标系中,将二次函数y=3x2的图象向左平移2个单位,所得图象的解析式为( )
| A、y=3x2-2 |
| B、y=3x2+2 |
| C、y=3(x-2)2 |
| D、y=3(x+2)2 |
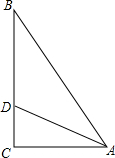 (1)计算:
(1)计算: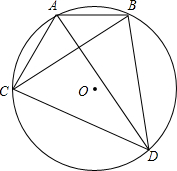 如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为
如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为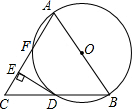 AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证:
AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使BD=DC,连AC,过D作DE⊥AC于E,AC交⊙O于F.求证: 如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少?
如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少? 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( )