题目内容
 已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.
已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.考点:角平分线的定义
专题:
分析:首先根据∠ABE:∠CBE=1:4,设∠ABE=x°,∠CBE=4x°,则∠ABC=5x°,再根据角平分线的性质可得∠ABD=2.5x°,∠DBE=1.5x°,由条件∠DBE=45°,可得方程1.5x=45,计算出x的值,然后可得∠ABC的度数.
解答:解:∵∠ABE:∠CBE=1:4,
∴设∠ABE=x°,∠CBE=4x°,
∴∠ABC=5x°,
∵BD平分∠ABC,
∴∠ABD=2.5x°,
∴∠DBE=1.5x°,
∵∠DBE=45°,
∴1.5x=45,
解得:x=30,
∴∠ABC=5×30°=150°.
∴设∠ABE=x°,∠CBE=4x°,
∴∠ABC=5x°,
∵BD平分∠ABC,
∴∠ABD=2.5x°,
∴∠DBE=1.5x°,
∵∠DBE=45°,
∴1.5x=45,
解得:x=30,
∴∠ABC=5×30°=150°.
点评:此题主要考查了角平分线的性质,关键是掌握方程思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,将二次函数y=3x2的图象向左平移2个单位,所得图象的解析式为( )
| A、y=3x2-2 |
| B、y=3x2+2 |
| C、y=3(x-2)2 |
| D、y=3(x+2)2 |
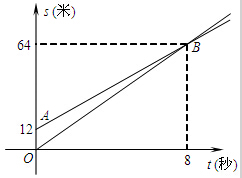 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( ) 一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.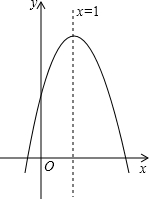 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )