题目内容
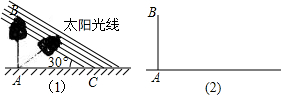
某数学兴趣小组,利用树影量树高,如图(1)所示,已测出树AB的影长AC为12m,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,求树与地面成45°角的影长.(用图(2)解答)
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,求树与地面成45°角的影长.(用图(2)解答)

考点:平行投影
专题:计算题
分析:(1)在Rt△ABC中,根据含30度的直角三角形三边的关系求解;
(2)先画出几何图形,如图,作AH⊥BC于H,在Rt△ABH中,由于∠ABH=45°,根据等腰直角三角形的性质得AH=BH=
AB=2
,在Rt△ACH中据含30度的直角三角形三边的关系得到CH=
AH=6
,然后计算BC即可.
(2)先画出几何图形,如图,作AH⊥BC于H,在Rt△ABH中,由于∠ABH=45°,根据等腰直角三角形的性质得AH=BH=
| ||
| 2 |
| 6 |
| 3 |
| 2 |
解答:解:(1)在Rt△ABC中,
∵∠ACB=30°,
∴AB=
AC=
×12=4
(m),
即树高为4
m;
(2)如图,作AH⊥BC于H,

在Rt△ABH中,∵∠ABH=45°,
∴AH=BH=
AB=
×4
=2
,
在Rt△ACH中,∵∠ACH=30°,
∴CH=
AH=
×2
=6
,
∴BC=BH+CH=(2
+6
)m,
即树与地面成45°角的影长为(2
+6
)m.
∵∠ACB=30°,
∴AB=
| ||
| 3 |
| ||
| 3 |
| 3 |
即树高为4
| 3 |
(2)如图,作AH⊥BC于H,

在Rt△ABH中,∵∠ABH=45°,
∴AH=BH=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 6 |
在Rt△ACH中,∵∠ACH=30°,
∴CH=
| 3 |
| 3 |
| 6 |
| 2 |
∴BC=BH+CH=(2
| 6 |
| 2 |
即树与地面成45°角的影长为(2
| 6 |
| 2 |
点评:本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.也考查了解直角三角形.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知关于x的方程3x+a-8=0的解是x=2,则a的值是( )
| A、2 | B、3 | C、4 | D、5 |
在平面直角坐标系中,将二次函数y=3x2的图象向左平移2个单位,所得图象的解析式为( )
| A、y=3x2-2 |
| B、y=3x2+2 |
| C、y=3(x-2)2 |
| D、y=3(x+2)2 |
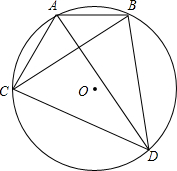 如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为
如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为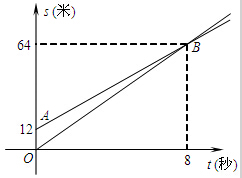 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: