题目内容
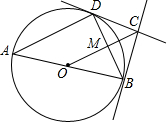 如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.
如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.考点:切线的判定
专题:证明题
分析:连结OD,如图,根据圆周角定理,由AB为⊙O的直径得到∠ADB=90°,易得OM为△ABD的中位线,则OM∥AD,所以∠BMO=∠ADB=90°,于是可判断OC垂直平分BD,根据线段垂直平分线的性质得CD=CB,则∠1=∠2,加上∠3=∠4,所以∠CBO=∠CDO=90°,然后根据切线的判定定理得到CD是⊙O的切线.
解答:证明: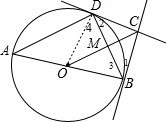 连结OD,如图,
连结OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵点M为BD的中点,O点为AB的中点,
∴OM为△ABD的中位线,
∴OM∥AD,
∴∠BMO=∠ADB=90°,
∴OC垂直平分BD,
∴CD=CB,
∴∠1=∠2,
而OB=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠CBO=∠CDO,
∵BC⊥AB,
∴∠CBO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线.
 连结OD,如图,
连结OD,如图,∵AB为⊙O的直径,
∴∠ADB=90°,
∵点M为BD的中点,O点为AB的中点,
∴OM为△ABD的中位线,
∴OM∥AD,
∴∠BMO=∠ADB=90°,
∴OC垂直平分BD,
∴CD=CB,
∴∠1=∠2,
而OB=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠CBO=∠CDO,
∵BC⊥AB,
∴∠CBO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
在平面直角坐标系中,将二次函数y=3x2的图象向左平移2个单位,所得图象的解析式为( )
| A、y=3x2-2 |
| B、y=3x2+2 |
| C、y=3(x-2)2 |
| D、y=3(x+2)2 |
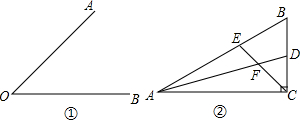
 如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,D为
如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,D为
 一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.