题目内容
10.已知3是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是菱形ABCD的两条对角线的长,则菱形ABCD的面积为4.5.分析 首先利用一元二次方程的解得出m的值,再利用根与系数的关系得出方程的两根之积,再结合菱形面积公式求出答案.
解答 解:∵3是关于x的方程x2-2mx+3m=0的一个根,
∴32-6m+3m=0,
解得:m=3,
∴原方程为:x2-6x+9=0,
∴方程的两根之积为:9,
∴菱形ABCD的面积为:4.5.
故答案为:4.5.
点评 此题主要考查了菱形的性质以及一元二次方程的解和根与系数的关系,正确得出方程的两根之积是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列计算,正确的是( )
| A. | -|-3|=-3 | B. | 30=0 | C. | 3-1=-$\frac{1}{3}$ | D. | $\root{3}{9}$=3 |
19.下列一元二次方程有两个相等实数根的是( )
| A. | x2+3=0 | B. | (x+1)2=0 | C. | x2+2x=0 | D. | (x+3)(x-1)=0 |
15.若|a|-|b|=0,则下列结论一定正确的是( )
| A. | a=b=0 | B. | a与b相等 | ||
| C. | a与b异号 | D. | a与b互为相反数或相等 |
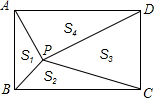 如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论的序号是②④.
如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论的序号是②④.