题目内容
2.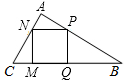 如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.
如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.(1)求证:PQ2=BQ•CM;
(2)若BQ=16,CM=9,求正方形的边长.
分析 (1)由四边形ABCD是正方形知PQ=MN,再证△CMN∽△PQB可得$\frac{CM}{PQ}$=$\frac{MN}{BQ}$,即$\frac{CM}{PQ}=\frac{PQ}{BQ}$,即可得出答案;
(2)将BQ=16、CM=9代入PQ2=BQ•CM即可得出答案.
解答 解:(1)∵四边形ABCD是正方形,
∴∠CMN=∠PQB=90°,PQ=MN,
∴∠C+∠CNM=90°,
又∵∠C+∠B=90°,
∴∠CNM=∠B,
则△CMN∽△PQB,
∴$\frac{CM}{PQ}$=$\frac{MN}{BQ}$,即$\frac{CM}{PQ}=\frac{PQ}{BQ}$,
则PQ2=BQ•CM;
(2)当BQ=16、CM=9时,
由PQ2=BQ•CM可得PQ2=16×9=144,
∵PQ>0,
∴PQ=12,即正方形的边长为12.
点评 本题主要考查相似三角形的判定与性质,熟练掌握正方形的性质及相似三角形的判定、性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.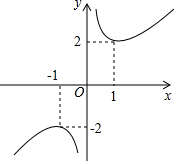 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )| A. | 该函数的图象是中心对称图形 | |
| B. | 当x>0时,该函数在x=1时取得最小值2 | |
| C. | 在每个象限内,y的值随x值的增大而减小 | |
| D. | y的值不可能为1 |
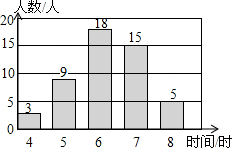 在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.
在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.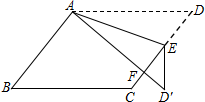 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.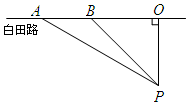 校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.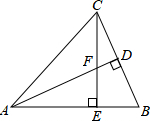 如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.
如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.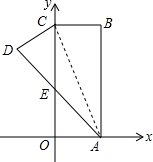 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).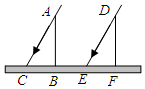 如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )