题目内容
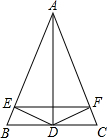 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:角平分线的性质,全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:根据角平分线的定义可得∠BAD=∠CAD,根据角平分线上的点到角的两边距离相等可得ED=FD,再利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应角相等可得∠ADE=∠ADF,全等三角形对应边相等可得AE=AF,再根据等腰三角形三线合一的性质可得AD垂直平分EF,但无法确定EF垂直平分AD.
解答:
解:∵AD平分∠BAC,
∴∠BAD=∠CAD,故(1)正确;
∵DE⊥AB,DF⊥AC,
∴ED=FD,故(2)正确;
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠ADE=∠ADF,AE=AF,
∴AD平分∠EDF,故(3)正确;
∵AD平分∠BAC,
∴AD垂直平分EF,
无法确定EF垂直平分AD,故(4)错误.
综上所述,正确的有(1)(2)(3)共3个.
故选C.
∴∠BAD=∠CAD,故(1)正确;
∵DE⊥AB,DF⊥AC,
∴ED=FD,故(2)正确;
在Rt△ADE和Rt△ADF中,
|
∴Rt△ADE≌Rt△ADF(HL),
∴∠ADE=∠ADF,AE=AF,
∴AD平分∠EDF,故(3)正确;
∵AD平分∠BAC,
∴AD垂直平分EF,
无法确定EF垂直平分AD,故(4)错误.
综上所述,正确的有(1)(2)(3)共3个.
故选C.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟练掌握各性质并准确识图确定出全等三角形是解题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图是某单元楼居民六月份的用电(单位:度)情况,则关于用电量描述不正确的是( )
如图是某单元楼居民六月份的用电(单位:度)情况,则关于用电量描述不正确的是( )| A、众数为30 |
| B、中位数为25 |
| C、平均数为24 |
| D、方差为83 |
 如图,在四边形ABCD中,对角线AC、BD相交于点O.AB=AD,CB=CD,则图中全等三角形共有( )
如图,在四边形ABCD中,对角线AC、BD相交于点O.AB=AD,CB=CD,则图中全等三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
不等式组
的解集为( )
|
| A、-2≤x≤1 | B、-2<x<1 |
| C、x≥1 | D、x≥2 |
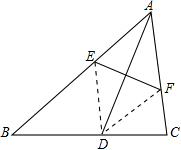 如图,在三角形纸片ABC中,AD是△ABC的角平分线,把△ABC进行折叠,使点A与点D重合,折痕与AB相交于E,与AC相交于F,求证:四边形AEDF是菱形.
如图,在三角形纸片ABC中,AD是△ABC的角平分线,把△ABC进行折叠,使点A与点D重合,折痕与AB相交于E,与AC相交于F,求证:四边形AEDF是菱形.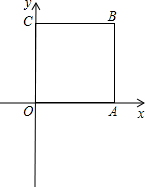 如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.
如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.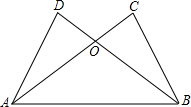 如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.
如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.