题目内容
如图所示，扳手的开口a的值为2| 3 |
| A、2cm | ||||
B、
| ||||
C、
| ||||
| D、1cm |
考点：正多边形和圆
专题：
分析：设正六边形的中心为点O，过点O作OD⊥AD于点D，连接OA，根据a=2
可知OD=
，由直角三角形的性质求出OA的长即可．
| 3 |
| 3 |
解答：
解：设正六边形的中心为点O，过点O作OD⊥AD于点D，连接OA，
∵a=2
cm，
∴OD=
cm．
∵∠AOD=
=30°，
∴OA=
=
=2（cm）．
故选A．
解：设正六边形的中心为点O，过点O作OD⊥AD于点D，连接OA，∵a=2
| 3 |
∴OD=
| 3 |
∵∠AOD=
| 60° |
| 2 |
∴OA=
| OD |
| cos30° |
| ||||
|
故选A．
点评：本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
若m是方程x2+x-1=0的根，则2m2+2m+2011的值为（ ）
| A、2010 | B、2011 |
| C、2012 | D、2013 |
如图，已知AB=DE，AB∥DE，AF=DC．求证：BC∥EF．
如图，矩形ABCD中，对角线AC、BD交于点O，AB=6，∠BAC=60°，DE⊥AC交BC于E，则DE的长为（ ）| A、2 | ||
B、4
| ||
C、2
| ||
D、3
|
如图是某单元楼居民六月份的用电（单位：度）情况，则关于用电量描述不正确的是（ ）| A、众数为30 |
| B、中位数为25 |
| C、平均数为24 |
| D、方差为83 |
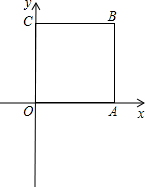如图，四边形OABC为正方形，A（2，0），C（0，2），直线y=3x+m与线段OA、BC相交，且将正方形OABC的面积分成1：2两部分，求m的值．