题目内容
 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?考点:相似三角形的应用
专题:
分析:过A作AM⊥DE于M,交BC与N,则AN=0.08m,AM=2m,求出△ABC∽△ADE,利用相似三角形对应高的比等于相似比解答即可.
解答:
解:如图,过A作AM⊥DE于M,交BC与N ,AN=0.08m,AM=2m,
,AN=0.08m,AM=2m,
由于房间的地面为边长为4m的正方形,则DE=4
m,
∵BC∥DE,
∴△ABC∽△ADE,
∴
=
,即
=
,
∴BC≈0.23.
答:灯罩的直径BC约为0.23m.
 ,AN=0.08m,AM=2m,
,AN=0.08m,AM=2m,由于房间的地面为边长为4m的正方形,则DE=4
| 2 |
∵BC∥DE,
∴△ABC∽△ADE,
∴
| BC |
| DE |
| AN |
| AM |
| BC | ||
4
|
| 0.08 |
| 2 |
∴BC≈0.23.
答:灯罩的直径BC约为0.23m.
点评:本题考查了相似三角形的应用,中心投影,掌握相似三角形对应高的比等于相似比是解题的关键,计算时注意单位要统一.

练习册系列答案
相关题目
 如图,将三角尺的直角顶点放在直尺的一边上,若∠1=30°,∠2=50°,则∠3的度数等于( )
如图,将三角尺的直角顶点放在直尺的一边上,若∠1=30°,∠2=50°,则∠3的度数等于( )| A、20° | B、30° |
| C、50° | D、55° |
 如图,已知AB=DE,AB∥DE,AF=DC.求证:BC∥EF.
如图,已知AB=DE,AB∥DE,AF=DC.求证:BC∥EF.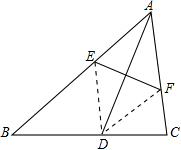 如图,在三角形纸片ABC中,AD是△ABC的角平分线,把△ABC进行折叠,使点A与点D重合,折痕与AB相交于E,与AC相交于F,求证:四边形AEDF是菱形.
如图,在三角形纸片ABC中,AD是△ABC的角平分线,把△ABC进行折叠,使点A与点D重合,折痕与AB相交于E,与AC相交于F,求证:四边形AEDF是菱形.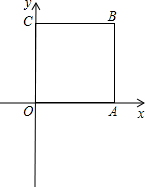 如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.
如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.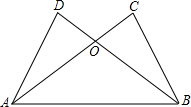 如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.
如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.