题目内容
 如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.
如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.(1)猜想AQ与PA的大小关系,并说明理由;
(2)按三角形内角判断△QAP的类型,并说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)易证∠ABQ=∠ACQ,即可证明△ABP≌△QCA,可得AQ=AP,即可解题;
(2)易证∠CAQ=∠P和∠AQP=∠CAQ,即可求得∠P=∠AQP=∠CAQ=45°,即可解题.
(2)易证∠CAQ=∠P和∠AQP=∠CAQ,即可求得∠P=∠AQP=∠CAQ=45°,即可解题.
解答:证明:如图:

(1)∵∠BQF+∠ABQ=90°,∠ACQ+∠CQE=90°,∠BQF=∠CQE,
∴∠ABQ=∠ACQ,
在△ABP和△QCA中,
,
∴△ABP≌△QCA(SAS),
∴AQ=AP;
(2)∵△ABP≌△QCA,
∴∠CAQ=∠P,
∵AQ=AP,
∴∠AQP=∠P,
∴∠AQP=∠CAQ,
∵∠AEQ=90°,
∴∠P=∠AQP=∠CAQ=45°,
∴△QAP为等腰直角三角形.

(1)∵∠BQF+∠ABQ=90°,∠ACQ+∠CQE=90°,∠BQF=∠CQE,
∴∠ABQ=∠ACQ,
在△ABP和△QCA中,
|
∴△ABP≌△QCA(SAS),
∴AQ=AP;
(2)∵△ABP≌△QCA,
∴∠CAQ=∠P,
∵AQ=AP,
∴∠AQP=∠P,
∴∠AQP=∠CAQ,
∵∠AEQ=90°,
∴∠P=∠AQP=∠CAQ=45°,
∴△QAP为等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABP≌△QCA是解题的关键.

练习册系列答案
相关题目
“神舟五号”飞船发射前,一远洋测量船从基地A沿南偏西40°方向到目标区域B执行跟踪测量任务.任务完成后,测量船沿原路返回基地A,则返回时航行方向是( )
| A、北偏西50° |
| B、北偏东40° |
| C、北偏西40° |
| D、北偏东50° |
 已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y=
已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y=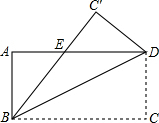 如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E.
如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E.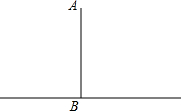 地面上直立一根标杆AB如图,杆长为2cm.
地面上直立一根标杆AB如图,杆长为2cm.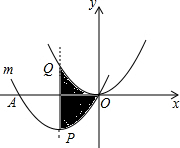 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为
如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为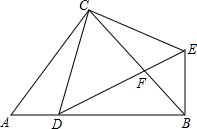 如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F.
如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F.