题目内容
 把一块直尺与一块三角板如图放置,若∠1=30°,则∠2的度数为
把一块直尺与一块三角板如图放置,若∠1=30°,则∠2的度数为考点:平行线的性质,三角形的外角性质
专题:
分析:根据直角三角形两锐角互余求出∠3,再根据邻补角定义求出∠4,然后根据两直线平行,同位角相等解答即可.
解答:解:∵∠1=30°,
∴∠3=90°-∠1=90°-30°=60°,
∴∠4=180°-60°=120°,
∵直尺的两边互相平行,
∴∠2=∠4=120°.
故答案为:120°
∴∠3=90°-∠1=90°-30°=60°,
∴∠4=180°-60°=120°,
∵直尺的两边互相平行,
∴∠2=∠4=120°.
故答案为:120°
点评:本题考查了平行线的性质,直角三角形两锐角互余的性质,邻补角的定义,是基础题,准确识图是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知反比例函数y=
,一次函数y=
x+k+n,若它们的图象对于任意的非零实数k都只有一个公共点,则m,n的值分别为( )
| k |
| x |
| km |
| 4 |
| A、m=-1,n=0 |
| B、m=0,n=-1 |
| C、m=1,n=-1 |
| D、m=-1,n=1 |
 如图,若三角形ABC中经平移后任意一点P(x,y)的对应点为P1(x+5,y-3),则点A的对应点A1的坐标是( )
如图,若三角形ABC中经平移后任意一点P(x,y)的对应点为P1(x+5,y-3),则点A的对应点A1的坐标是( )| A、(4,1) |
| B、(9,-4) |
| C、(-6,7) |
| D、(-1,2) |
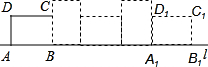 矩形ABCD的边AB=4,AD=3,现将矩形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当它翻滚至类似开始的位置时A1B1C1D1(如图所示),则顶点D所经过的路线长是
矩形ABCD的边AB=4,AD=3,现将矩形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当它翻滚至类似开始的位置时A1B1C1D1(如图所示),则顶点D所经过的路线长是 如图,已知梯形OABC的底边D在x轴上,CB∥OA,BA⊥OA,过点C的双曲线
如图,已知梯形OABC的底边D在x轴上,CB∥OA,BA⊥OA,过点C的双曲线