题目内容
10.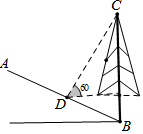 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
分析 根据题意首先利用勾股定理得出DF,DE的长,再利用锐角三角函数关系得出EC的长,进而得出答案.
解答 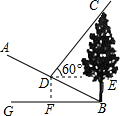 解:过点D作DF⊥BG,垂足为F,
解:过点D作DF⊥BG,垂足为F,
∵斜坡AB的坡度i=1:2,
∴设DF=x,BF=2x,则DB=10m,
∴x2+(2x)2=102,
解得:x=2$\sqrt{5}$,
故DE=4$\sqrt{5}$,BE=DF=2$\sqrt{5}$,
∵测得太阳光线与水平线的夹角为60°,
∴tan60°=$\frac{EC}{DE}$=$\frac{EC}{4\sqrt{5}}$=$\sqrt{3}$,
解得:EC=4$\sqrt{15}$,
故BC=EC+BE=(2$\sqrt{5}$+4$\sqrt{15}$)(m).
点评 此题主要考查了解直角三角形的应用以及勾股定理,正确得出DF的长是解题关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
5.某超市在“十一”期间对顾客实行优惠购物的条款如下表:
(1)甲顾客一次性购物800元,他实际付款690元.
(2)乙顾客在该超市一次性购物x元,当200≤x<500时,他实际付款0.9x元;当x≥500时,他实际付款(0.8x+50)元;(用含x的代数式表示)
(3)丙顾客两次购物货款合计为820元,第一次购物的货款为a元(200<a<300),试用a的代数式表示丙顾客两次购物实际付款合计多少元?
| 一次性购物 | 优惠办法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠; 超过500元部分给予八折优惠 |
(2)乙顾客在该超市一次性购物x元,当200≤x<500时,他实际付款0.9x元;当x≥500时,他实际付款(0.8x+50)元;(用含x的代数式表示)
(3)丙顾客两次购物货款合计为820元,第一次购物的货款为a元(200<a<300),试用a的代数式表示丙顾客两次购物实际付款合计多少元?
2.二次函数y=(x-1)2-2的顶点坐标是( )
| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,2) |
19.某蔬菜生产基地经市场调查,对种植的A、B、C三种蔬菜的成本与售价情况统计如表:
并且从市场调研中总结得知:该基地的蔬菜C的种植面积一般是蔬菜B种植面积的2倍,生产基地要按照这个规律种植,才不至于滞销.现知道基地共有用地200亩,蔬菜A每亩产量为3吨,蔬菜B每亩产量为5吨,蔬菜C每亩产量为7吨.若设种植蔬菜B为x亩,基地假设把生产的蔬菜都能销售出去,其利润为y元.
(1)求y与x之间的函数关系式;
(2)根据市场行情,蔬菜A的种植不能多于50亩,求该蔬菜生产基地在这次种植中能获得的最大利润.
| 蔬菜品种 | A | B | C |
| 成本(元/吨) | 3000 | 2200 | 1500 |
| 售价(元/吨) | 7000 | 4000 | 3200 |
(1)求y与x之间的函数关系式;
(2)根据市场行情,蔬菜A的种植不能多于50亩,求该蔬菜生产基地在这次种植中能获得的最大利润.
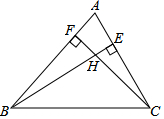 在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,
在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,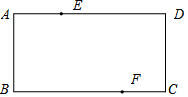 如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形.
如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形. 在平面直角坐标系上画出y=2x-2的图象
在平面直角坐标系上画出y=2x-2的图象