题目内容
9. 如图,?ABCD中,AB=4,BC=8,点E,F分别在BC,CD边上,且∠EAF=∠ABC=60°.
如图,?ABCD中,AB=4,BC=8,点E,F分别在BC,CD边上,且∠EAF=∠ABC=60°.(1)求证:AC⊥CD;
(2)若BE=3,求DF的长.
(3)设△AEF的面积为S,求S的取值范围.
分析 (1)过点A作AG⊥BC,首先利用勾股定理和三角函数求出∠BAG,AG,BG,CG,其次,求出∠CAG,从而得出结论;
(2)先由勾股定理求出AG,EG,AC,再判断出△AEG∽△AFC,得出比例式代值求出FC;
(3)先判断出三角形AEF面积最小和最大时的位置,根据三角形的面积公式求解即可.
解答 解:(1)如图,
过点A作AG⊥BC,
在Rt△AGB中,∠ABC=60°,AB=4,
∴∠BAG=30°,BG=2,AG=2$\sqrt{3}$,
∵BC=8,
∴CG=BC-BG=6,
在Rt△ACG中,tan∠CAG=$\frac{CG}{AG}$=$\frac{6}{2\sqrt{3}}$=$\sqrt{3}$,
∴锐角∠CAG=60°,
∴∠BAC=∠BAG+∠CAG=30°+60°=90°,
∴AC⊥CD;
(2)如图,
过点A作AG⊥BC,
由(1)得,AG=2$\sqrt{3}$,BG=2,
∵BE=3,
∴EG=1,
在Rt△ACG中,AC=2AG=4$\sqrt{3}$,
由(1)得,∠CAG=∠EAG+∠CAE=60°,
∵∠EAF=∠CAE+∠CAF=60°,
∴∠EAG=∠CAF,
在平行四边形ABCD中,CD=AB=4,AB∥DC,
∵∠BAC=90°,
∴∠ACF=∠BAC=90°,
∴△AEG∽△AFC,
∴$\frac{AG}{AC}=\frac{EG}{CF}$,
∴$\frac{2\sqrt{3}}{4\sqrt{3}}=\frac{1}{CF}$,
∴CF=2,
∵CD=4,
∴DF=2;
(3)∵BC>CD,而点E在BC上,点F在CD上,
∴当点F与点C重合时,
∵∠CAG=∠EAF=60°,
∴S=S△ACG最小,
由(1)、(2)有,CG=6,AG=2$\sqrt{3}$,
∴S△ACG=$\frac{1}{2}$CG×AG=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$,
当点F与点D重合时,此时点E仍在BC上,此时S最大,
∴S最大=$\frac{1}{2}$×AD×AG=$\frac{1}{2}$×8×2$\sqrt{3}$=8$\sqrt{3}$;
∴6$\sqrt{3}$≤S≤8$\sqrt{3}$.
点评 此题是四边形综合题,主要考查了平行四边形的性质,垂直的判断方法,相似三角形的性质和判定,勾股定理,三角函数,判断△AEG∽△AFC是解本题的关键,也是难点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 四边形中至多有一个角是钝角或直角 | |
| B. | 四边形中至少有两个角是钝角或直角 | |
| C. | 四边形中四个角都是钝角或直角 | |
| D. | 四边形中没有一个角是钝角或直角 |
| A. | a-5<b-5 | B. | 2+a<2+b | C. | 3a>3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
| 气温(℃) | 34 | 32 | 31 | 30 | 29 | 28 | 27 | 25 | 24 | 23 | 22 | 14 |
| 天数 | 1 | 1 | 4 | 4 | 6 | 4 | 3 | 2 | 2 | 1 | 2 | 1 |
 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F, 已知,如图:?ABCD中,对角线相交于O点,AB⊥AC,AB=AC,沿对角线AC将△ABC翻折至△AEC,EC与AD相交于F.
已知,如图:?ABCD中,对角线相交于O点,AB⊥AC,AB=AC,沿对角线AC将△ABC翻折至△AEC,EC与AD相交于F. 已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.
已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.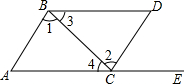 如图,点E在AC的延长线上,下列条件①∠3=∠4,②∠1=∠2,③∠D=∠ACD,④∠D+∠ACD=180°中,能判断AB∥CD的是②(填序号即可).
如图,点E在AC的延长线上,下列条件①∠3=∠4,②∠1=∠2,③∠D=∠ACD,④∠D+∠ACD=180°中,能判断AB∥CD的是②(填序号即可).