题目内容
7.如图,在△ABC中,AB=AC=6,AB的垂直平分线交AB于点E,交BC于点D,连接AD,若AD=4,则DC=5.
分析 过A作AF⊥BC于F,根据等腰三角形的性质得到BF=CF=$\frac{1}{2}$BC,由AB的垂直平分线交AB于点E,得到BD=AD=4,设DF=x,根据勾股定理列方程即可得到结论.
解答 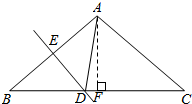 解:过A作AF⊥BC于F,
解:过A作AF⊥BC于F,
∵AB=AC,
∴BF=CF=$\frac{1}{2}$BC,
∵AB的垂直平分线交AB于点E,
∴BD=AD=4,
设DF=x,
∴BF=4+x,
∵AF2=AB2-BF2=AD2-DF2,
即16-x2=36-(4+x)2,
∴x=0.5,
∴DF=0.5,
∴CD=CF+DF=BF+DF=BD+2DF=4+0.5×2=5,
故答案为:5.
点评 此题考查了等腰三角形的性质,线段垂直平分线的性质.此题难度不大,注意掌握转化思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.用反证法证明真命题“四边形中至少有一个角是钝角或直角”时,应假设( )
| A. | 四边形中至多有一个角是钝角或直角 | |
| B. | 四边形中至少有两个角是钝角或直角 | |
| C. | 四边形中四个角都是钝角或直角 | |
| D. | 四边形中没有一个角是钝角或直角 |
16. 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )| A. | a>0 | B. | c>0 | C. | b2-4ac>0 | D. | a+b+c>0 |

 某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.
某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7. 某校根据去年七年级学生参加某次考试的数学成绩的等级,绘制成如图所示的扇形统计图,则图中表示A等级的扇形圆心角的度数为108°.
某校根据去年七年级学生参加某次考试的数学成绩的等级,绘制成如图所示的扇形统计图,则图中表示A等级的扇形圆心角的度数为108°.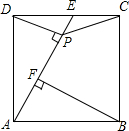 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,