题目内容
14.已知一次函数的图象经过点(-1,-5),且与正比例函数y=$\frac{1}{2}$x的图象相交于点(2,a).求这个一次函数的图象与y轴的交点坐标.分析 设该一次函数的解析式为y=kx+b(k≠0),将点(2,a) 代入y=$\frac{1}{2}$x中可得出a的值,再由点(2,1)、(-1,-5)利用待定系数法即可求出直线的解析式,令该直线解析式中x=0求出y值即可得出结论.
解答 解:设该一次函数的解析式为y=kx+b(k≠0),
把(2,a) 代入y=$\frac{1}{2}$x,得:a=1,
把(2,1)、(-1,-5)代入y=kx+b中,
得:$\left\{{\begin{array}{l}{2k+b=1}\\{-k+b=-5}\end{array}}\right.$,解得:$\left\{{\begin{array}{l}{k=2}\\{b=-3}\end{array}}\right.$,
∴y=2x-3.
令y=2x-3中x=0,则y=-3,
∴一次函数y=kx+b的图象与y轴的交点坐标(0,-3).
点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键是利用待定系数法求出该直线的解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某班气象兴趣小组的同学对北京市2016年5月份每天的最高气温做了统计,如表:
那么北京市5月份每天最高气温的众数是29℃,中位数是29℃.
| 气温(℃) | 34 | 32 | 31 | 30 | 29 | 28 | 27 | 25 | 24 | 23 | 22 | 14 |
| 天数 | 1 | 1 | 4 | 4 | 6 | 4 | 3 | 2 | 2 | 1 | 2 | 1 |
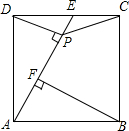 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F, 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.求证:DE⊥BE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.求证:DE⊥BE.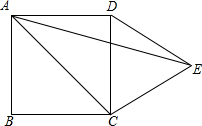 如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°.
如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°. 如图,菱形ABCD的两条对角线相交于点O,∠DAC=30°,BD=12
如图,菱形ABCD的两条对角线相交于点O,∠DAC=30°,BD=12 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O (0,0),A (2,4),B (4,0),分别将点A、B的横坐标、纵坐标都乘以1.5,得相应的点A'、B'的坐标.
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O (0,0),A (2,4),B (4,0),分别将点A、B的横坐标、纵坐标都乘以1.5,得相应的点A'、B'的坐标.