题目内容
16. 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点.若点E,F分别是AB,AC上的点,且∠EDF=90°,下列结论中正确结论的个数是( )
如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点.若点E,F分别是AB,AC上的点,且∠EDF=90°,下列结论中正确结论的个数是( )①△AED≌△CFD ②(BE+CF)=$\frac{\sqrt{2}}{2}$BC ③S△AEF≤$\frac{1}{4}$S△ABC ④S四边形AEDF=AD•EF.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据直角三角形斜边中线等于斜边一半得AD=DC,由三线合一及等腰直角三角形得∠BAD=∠C=45°,再证∠EDA=∠FDC,则△AED≌△CFD;
②根据全等可知:AE=CF,并由三角函数得:AB=$\frac{\sqrt{2}}{2}$BC,代入AB=AE+BE中即可;
③设AB=AC=a,AE=CF=x,计算△AEF的面积并求最大值,与$\frac{1}{4}$S△ABC 对比,可知结论正确;
④因为四边形AEDF的面积是△ADE和△ADF面积的和,由①知:△AED≌△CFD,则面积也相等,所以四边形AEDF的面积就是△ADC的面积,则四边形AEDF的面积=$\frac{1}{2}$AD•DC,则结论错误.
解答 解:①∵∠BAC=90°,D为BC的中点,
∴AD=DC=$\frac{1}{2}$BC,
∵AB=AC,
∴∠BAD=∠DAC=$\frac{1}{2}$×90°=45°,∠C=45°,
∴∠BAD=∠C,
∵∠EDF=90°,
∴∠EDA+∠ADF=90°,
∵∠FDC+∠ADF=90°,
∴∠EDA=∠FDC,
∴△AED≌△CFD,
所以选项①正确;
②由△AED≌△CFD得:AE=FC,
∴BE+CF=BE+AE=AB,
∵AB=AC,∠BAC=90°,
∴BC=$\sqrt{2}$AB,
∴AB=$\frac{\sqrt{2}}{2}$BC,
∴BE+CF=$\frac{\sqrt{2}}{2}$BC,
所以选项②正确;
③设AB=AC=a,AE=CF=x,则AF=a-x,
∴S△AEF=$\frac{1}{2}$AE•AF,
=$\frac{1}{2}$x(a-x),
=-$\frac{1}{2}$(x-$\frac{1}{2}$a)2+$\frac{1}{8}{a}^{2}$,
∴当x=$\frac{1}{2}$a时,S△AEF有最大值为$\frac{1}{8}{a}^{2}$,
∵S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}{a}^{2}$,
∴S△AEF≤$\frac{1}{4}$S△ABC,
所以选项③正确;
④∵S四边形AEDF=S△ADE+S△ADF,
=S△DFC+S△ADF,
=S△ADC,
=$\frac{1}{2}$AD•DC,
而EF与$\frac{1}{2}$DC不相等,所以选项④错误.
∴本题正确结论的个数是3个,
故选C.
点评 本题考查了全等三角形的性质和判定.等腰直角三角形的性质及三角形的面积计算,熟练掌握全等三角形的性质和判定是解题的关键;理解不规则四边形的面积由和的形式转化为一个三角形的面积,把三角形面积大小的比较转化为二次函数的最值问题,使问题得以解决.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )
某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )| A. | 0.96时 | B. | 1.07时 | C. | 1.15时 | D. | 1.50时 |
 某校根据去年七年级学生参加某次考试的数学成绩的等级,绘制成如图所示的扇形统计图,则图中表示A等级的扇形圆心角的度数为108°.
某校根据去年七年级学生参加某次考试的数学成绩的等级,绘制成如图所示的扇形统计图,则图中表示A等级的扇形圆心角的度数为108°.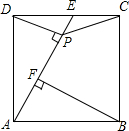 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
 已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.
已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$. 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.求证:DE⊥BE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.求证:DE⊥BE. 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O (0,0),A (2,4),B (4,0),分别将点A、B的横坐标、纵坐标都乘以1.5,得相应的点A'、B'的坐标.
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O (0,0),A (2,4),B (4,0),分别将点A、B的横坐标、纵坐标都乘以1.5,得相应的点A'、B'的坐标.