题目内容
5. 甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:| 甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
| 乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是7,中位数是7.5.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
分析 (1)根据表格中的数据可以将折线统计图补充完整;
(2)根据表格中的数据可以得到乙运动员射击训练成绩的众数和中位数;
(3)根据表格中的数据可以计算出甲运动员射击成绩的平均数和方差,根据甲乙两人的方差可以得到谁的稳定性好.
解答  解:(1)由表格中的数据可以将折线统计图补充完成,如右图所示,
解:(1)由表格中的数据可以将折线统计图补充完成,如右图所示,
(2)将乙的射击成绩按照从小到大排列是:
6,7,7,7,7,8,9,9,10,10,
故乙运动员射击训练成绩的众数是7,中位数是:$\frac{7+8}{2}$=7.5,
故答案为:7,7.5;
(3)由表格可得,
$\overline{{x}_{甲}}=\frac{8+9+7+9+8+6+7+8+10+8}{10}$=8,
${{S}_{甲}}^{2}=\frac{(8-8)^{2}+(9-8)^{2}+(7-8)^{2}+(9-8)^{2}+(8-8)^{2}+(6-8)^{2}+(7-8)^{2}+(8-8)^{2}+(10-8)^{2}+(8-8)^{2}}{10}$=1.2,
∵1.2<1.8,
∴甲本次射击成绩的稳定性好,
即甲运动员射击成绩的平均数是8,方差是1.2,甲本次射击成绩的稳定性好.
点评 本题考查折线统计图、中位数、众数、平均数、方差,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
16. 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )| A. | a>0 | B. | c>0 | C. | b2-4ac>0 | D. | a+b+c>0 |
13.已知实数a、b,若a>b,则下列结论正确的是( )
| A. | a-5<b-5 | B. | 2+a<2+b | C. | 3a>3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
20. 某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )
某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )
 某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )
某学校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果如图所示,根据此条形统计图估计这一天该校学生平均课外阅读时间约为( )| A. | 0.96时 | B. | 1.07时 | C. | 1.15时 | D. | 1.50时 |

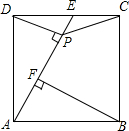 如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F,
如图,正方形ABCD中,点E为CD的中点,DP⊥AE,垂足为P点,BF⊥AE于F, 已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.
已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.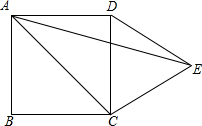 如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°.
如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°.