题目内容
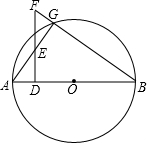如图，AB是⊙O的直径，FB交⊙O于点G，FD⊥AB，垂足为D，FD交AG于点E．求证：EF•DE=AE•EG．考点：相似三角形的判定与性质,圆周角定理
专题：证明题
分析：根据圆周角定理的运用和垂直的性质的运用，就可以得出△AED∽△FEG，由学生三角形的性质就可以得出结论．
解答：证明：∵AB是⊙O的直径，
∴∠AGB=90°．
∴∠EGF=90°
∵FD⊥AB，
∴∠ADE=90°，
∴∠EGF=∠ADE．
∵∠FEG=∠AED，
∴△FEG∽△AED．
∴
=
，
∴EF•DE=AE•EG．
∴∠AGB=90°．
∴∠EGF=90°
∵FD⊥AB，
∴∠ADE=90°，
∴∠EGF=∠ADE．
∵∠FEG=∠AED，
∴△FEG∽△AED．
∴
| EF |
| EA |
| EG |
| ED |
∴EF•DE=AE•EG．
点评：本题考查了圆周角定理的运用，垂直的性质的运用，相似三角形的判定及性质的运用，解答时证明三角形相似是关键．
练习册系列答案
相关题目
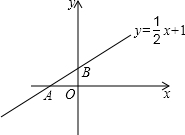如图，在平面直角坐标系中，直线
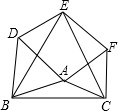如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形：△ABD，△BCE，△ACF，请解答下列问题：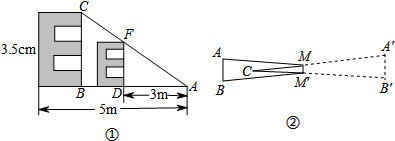
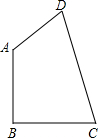如图，在四边形ABCD中，AB，BC，CD，DA的长分别为2，2，
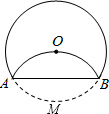如图，将⊙O沿AB折叠后，圆弧恰好经过圆心，求
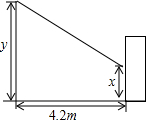我们知道，在同一时刻的物高与影长成比例．某兴趣小组利用这一知识进行实地测量，其中有一部分同学在某时刻测得竖立在地面上的一根长为1m的竹竿的影长是1.4m，另一部分同学在同一时刻对树影进行测量（如图），可惜树太靠近一幢建筑物（相距4.2m），树影不完全落在地面上，有一部分树影落在建筑物的墙壁上．
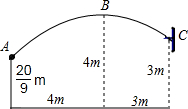如图，一场篮球赛中，球员甲跳起投篮，已知球出手时离地面