题目内容
1.己知点O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积等于2,求满足条件的点A的坐标.分析 分点A在x轴上和y轴上两种情况利用三角形的面积公式求出OA的长度,再分两种情况讨论求解.
解答 解:若点A在x轴上,则S△OAB=$\frac{1}{2}$×OA×2=2,
解得OA=2,
所以,点A的坐标为(2,0)或(-2,0),
若点A在y轴上,则S△OAB=$\frac{1}{2}$×OA×1=2,
解得OA=4,
所以,点A的坐标为(0,4)或(0,-4),
综上所述,点A的坐标为(2,0)或(-2,0)或(0,4)或(0,-4).
点评 本题考查了坐标与图形性质及三角形的面积,根据点A位于不同的数轴分类讨论是解题的关键.

练习册系列答案
相关题目
3.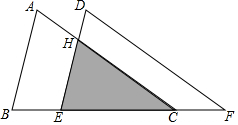 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$-$\frac{\sqrt{6}}{2}$ |
6.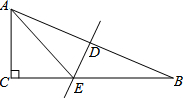 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )| A. | 15 | B. | 15$\sqrt{2}$ | C. | 30 | D. | 30$\sqrt{2}$ |
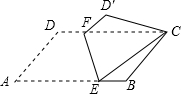 如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.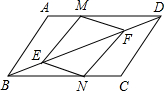 如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.
如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.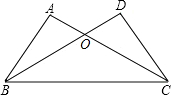 如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC.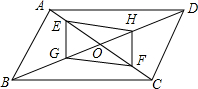 如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE.
如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE. 尺规作图,保留作图痕迹,不写作法.
尺规作图,保留作图痕迹,不写作法. 设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 $\widehat{BEC}$,以BC为直径作半圆$\widehat{BFC}$,则商标图案(阴影)面积等于$\frac{π}{6}$+$\sqrt{3}$cm2.
设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 $\widehat{BEC}$,以BC为直径作半圆$\widehat{BFC}$,则商标图案(阴影)面积等于$\frac{π}{6}$+$\sqrt{3}$cm2.