题目内容
4.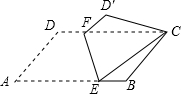 如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
分析 过点C作CG⊥AB的延长线于点G,易证△D′CF≌△ECB(ASA),从而可知D′F=EB,CF=CE,设AE=x,在△CEG中,利用勾股定理列出方程即可求出x的值.
解答 解: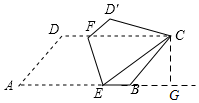 过点C作CG⊥AB的延长线于点G,
过点C作CG⊥AB的延长线于点G,
在?ABCD中,
∠D=∠EBC,AD=BC,∠A=∠DCB,
由于?ABCD沿EF对折,
∴∠D′=∠D=∠EBC,∠D′CE=∠A=∠DCB,
D′C=AD=BC,
∴∠D′CF+∠FCE=∠FCE+∠ECB,
∴∠D′CF=∠ECB,
在△D′CF与△ECB中,
$\left\{\begin{array}{l}{∠D′=∠EBC}\\{D′C=BC}\\{∠D′CF=∠ECB}\end{array}\right.$
∴△D′CF≌△ECB(ASA)
∴D′F=EB,CF=CE,
∵DF=D′F,
∴DF=EB,AE=CF
设AE=x,
则EB=6-x,CF=x,
∵BC=4,∠CBG=60°,
∴BG=$\frac{1}{2}$BC=2,
由勾股定理可知:CG=2$\sqrt{3}$,
∴EG=EB+BG=6-x+2=8-x
在△CEG中,
由勾股定理可知:(8-x)2+(2$\sqrt{3}$)2=x2,
解得:x=AE=$\frac{19}{4}$
故答案为:$\frac{19}{4}$
点评 本题考查平行四边形的综合问题,解题的关键是证明△D′CF≌△ECB,然后利用勾股定理列出方程,本题属于中等题型.

练习册系列答案
相关题目
14.今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:
则这20名同学年龄的众数和中位数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 5 | 7 |
| A. | 15,14 | B. | 15,15 | C. | 16,14 | D. | 16,15 |
12.已知△A′B′C′是由△ABC经过平移得到的,平移前后各顶点的坐标如下表所示.
(1)观察表中各对应点坐标的变化,并填空:a=0,b=2,c=9;
(2)在平面直角坐标系中画出△A'B'C'关于y轴对称的△A″B″C″.
| △ABC | A(a,0) | B(3,0) | C(5,5) |
| △A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(2)在平面直角坐标系中画出△A'B'C'关于y轴对称的△A″B″C″.
19.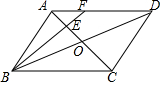 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )| A. | ①②③④ | B. | ①④ | C. | ②③④ | D. | ①②③ |
2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,如果汽车第一次右拐60°那么第二次拐弯应该( )
| A. | 左拐60° | B. | 右拐60° | C. | 左拐120° | D. | 右拐120° |
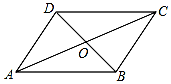 如图,在?ABCD中,对角线AC与BD相交于点O,△AOB的周长与△AOD的周长之和为12cm,两条对角线长之和为7cm,则这个平行四边形的周长为10cm.
如图,在?ABCD中,对角线AC与BD相交于点O,△AOB的周长与△AOD的周长之和为12cm,两条对角线长之和为7cm,则这个平行四边形的周长为10cm.