题目内容
10. 如图,Rt△ABC中,若∠ACB=90°,AC=4,BC=3,将△ABC绕着C点旋转,使得B点落在AB上的B′处,A点落在A′处,则AA′=$\frac{24}{5}$.
如图,Rt△ABC中,若∠ACB=90°,AC=4,BC=3,将△ABC绕着C点旋转,使得B点落在AB上的B′处,A点落在A′处,则AA′=$\frac{24}{5}$.
分析 由旋转的性质可证明△ACA′∽△BCB′,依据相似三角形的性质可得到AA′=$\frac{4}{3}$BB′,接下来,过点C作CD⊥AB,然后依据等腰三角形的性质和锐角三角函数的定义可求得BB′的长,从而得到问题的答案.
解答 解:过点C作CD⊥BB′.
∵BC=B′C
∵由旋转的性质可知:AC=A′C、∠BCB′=∠ACA′,BC=B′C,
∴△ACA′∽△BCB′.
∴AA′:BB′=4:3.
∴AA′=$\frac{4}{3}$BB′.
∵BC=B′C,DC⊥BB′,
∴BD=B′D.
∴BB′=2BD=2×3×$\frac{3}{5}$=$\frac{18}{5}$.
∴AA′=$\frac{18}{5}$×$\frac{4}{3}$=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题主要考查的是旋转的性质、相似三角形的判定和性质、锐角三角函数的定义、等腰三角形的性质,求得BB′的长以及AA′与BB′的关系是解题的关键.

练习册系列答案
相关题目
2.方程x2+x-12=0的两个根为( )
| A. | x1=-2,x2=6 | B. | x1=-6,x2=2 | C. | x1=-3,x2=4 | D. | x1=-4,x2=3 |
19.与$\sqrt{2}$是同类二次根式的为( )
| A. | $\sqrt{8}$ | B. | $\sqrt{3}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
20. 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
请根据上述统计图表,解答下列问题:
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:| 分 数 段 | 频数 | 频率 |
| 60≤x<70 | 9 | a |
| 70≤x<80 | 36 | 0.4 |
| 80≤x<90 | 27 | b |
| 90≤x≤100 | c | 0.2 |
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
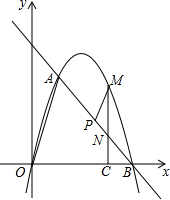 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.
如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点. 如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2$\sqrt{3}$),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为(1,$\sqrt{3}$).
如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2$\sqrt{3}$),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为(1,$\sqrt{3}$).