题目内容
1.如图,△ABC中,∠C=90°,⊙O为△ABC的内切圆,切点分别为D,E,F.(1)如图1,求sin∠DFE的值;
(2)如图2,若$\frac{BF}{AF}$=$\frac{2}{3}$,求sin∠DEF的值.
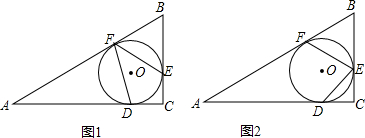
分析 (1)如图1所示:连接OD、OE.先证明四边形ODCE为矩形,从而得到∠EOD=90°,依据圆周角定理可得到∠EFD=45°,于是可得到sin∠EFD的值;
(2)如图所示;练级OE、DO、OF,OA.先证明四边形ODCE为正方形.EC=DC=r.由切线长定理可得到AC=3k+r,BC=2k+r,AB=5k,然后再△ABC中,依据勾股定理可求得:r=k,在依据勾股定理求得AO的长,由锐角三角函数的定义可得到sin∠FOA的值,然后根据∠AOF=∠FED,可求得sin∠FED的值.
解答 解:(1)如图1所示:连接OD、OE.
∵圆O为三角形的内切圆,
∴OD⊥AC,OE⊥BC,即∠ODC=∠OED=90°.
又∵∠C=90°,
∴四边形ODCE为矩形.
∴∠EFD=45°.
∴sin∠EFD=$\frac{\sqrt{2}}{2}$.
(2)如图所示,连接OE、DO、OF,OA.
由(1)可知四边形ODCE为矩形.
又∵OE=OF,
∴四边形ODCE为正方形.
∴EC=DC=r.
设BF=2k,AF=3k,则AD=3k,BE=2k,
∴AC=3k+r,BC=2k+r,AB=5k.
在△ABC中,由勾股定理得;AB2=AC2+BC2,即(5k)2=(3k+r)2+(2k+r)2.
解得:r=k.
∴OF=k.
在△AOF中,OA=$\sqrt{O{F}^{2}+O{A}^{2}}$=$\sqrt{10}$k.
∴sin∠FOA=$\frac{3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$.
∵∠AOF=$\frac{1}{2}$∠FOD,∠FED=$\frac{1}{2}$∠FOD,
∴∠AOF=∠FED.
∴sin∠FED=$\frac{3\sqrt{10}}{10}$.
点评 本题主要考查的是三角形的内切圆、锐角三角函数的定义、勾股定理、正方形的判定,用含k的式子表示出圆的半径的长度是解题的关键.

 学业测评一课一测系列答案
学业测评一课一测系列答案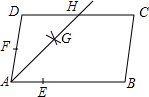 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )| A. | AG平分∠DAB | B. | AD=DH | C. | DH=BC | D. | CH=DH |
| A. | (x-2)4 | B. | (x2-2)2 | C. | (x2-4)2 | D. | (x+2)2(x-2)2 |
 如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是24.
如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是24. 发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.
发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.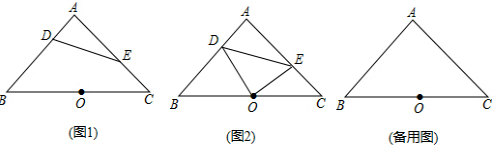
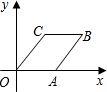 菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.
菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.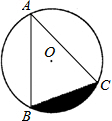 如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π).
如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π).