题目内容
13.如图,已知在等腰直角三角形ABC中,AB=AC=4,点D从点A出发,沿射线AB方向以每秒1个单位长的速度移动,同时点E从点C出发,沿射线CA方向以每秒1个单位长的速度移动.设点D移动的时间为t(秒).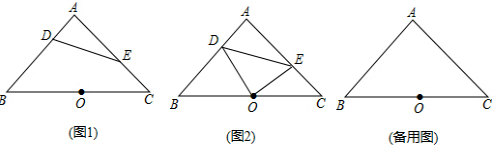
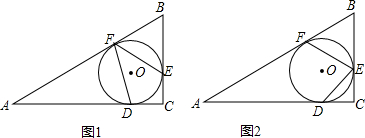
(1)如图1,当0<t<4时,连结DE,记△ADE的面积为S△ADE,则当t取何值时,S△ADE=2?
(2)如图2,点O为BC中点,连结OD、0E.
①当0<t<4时,小明探索发现S△ADE+SODE=$\frac{1}{2}$S△ABC,你认为他的发现正确吗?请做出判断并说明理由.
②当t>4时,请直接写出S△ADE,S△ODE,S△ABC之间的关系.
分析 (1)根据已知条件得到AD=t,AE=AC-CE=4-t,根据三角形的面积列方程即可得到结果;
(2)①如图2,连接AO,根据已知条件推出△AOE≌△BOD,于是得到S△AOE=S△BOD,等量代换得到结论;②如图2,连接AO,根据S四边形AEDO=S△AOE+S△DOE=S△ADE+S△BOD+S△ABO等量代换即可得到结论.
解答 解:(1)当0<t<4时,∵AD=t,AE=AC-CE=4-t,
∵∠A=90°,
∴S△ADE=$\frac{1}{2}$AD•AE=$\frac{1}{2}$t(4-t)=2,
解得:t=2,
∴当t=2时,S△ADE=2;
(2)①正确,如图2,连接AO,
∵AD=CE=t,
∴BD=AE=4-t,
∵△ABC是等腰直角三角形,点O为BC中点,
∴AO=BO,∠B=∠CAO=45°,
在△AOE与△BOD中,$\left\{\begin{array}{l}{BD=AE}\\{∠B=∠CAO}\\{OB=OA}\end{array}\right.$,
∴△AOE≌△BOD,
∴S△AOE=S△BOD,
∴S△ADE+SODE=S△AOE+S△AOD=S△BOD+S△AOD=S△ABO=$\frac{1}{2}$S△ABC;
②S△DOE-S△ADE=$\frac{1}{2}$S△ABC.
如图2,连接AO,
∵S四边形AEDO=S△AOE+S△DOE=S△ADE+S△BOD+S△ABO
由①证得S△AOE=S△BOD,
∴S△DOE=S△ADE+S△ABO,
即S△DOE-S△ADE=$\frac{1}{2}$S△ABC.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形面积的计算,证得△AOE≌△BOD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
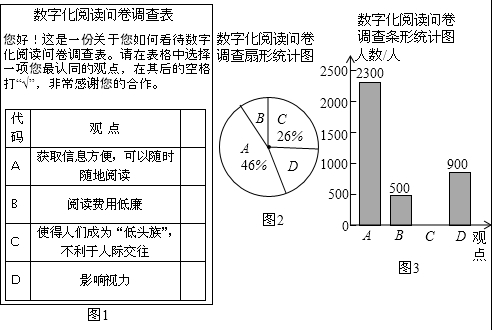
18.期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是85分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是85分”,上面两位同学的话能反映出的统计量是( )
| A. | 众数和中位数 | B. | 众数和平均数 | C. | 平均数和中位数 | D. | 众数和方差 |
5.为了了解某区的绿化进程,小明同学查询了园林绿化政务网,根据网站发布的近几年该城市城市绿化资源情况的相关数据,绘制了如下统计图(不完整)
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图
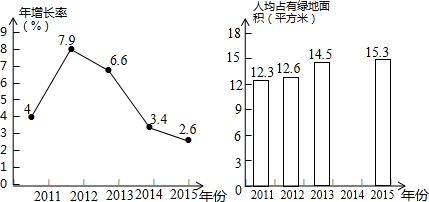
(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
如果按照小明的统计数据,请你通过计算估计,他所在学校的300名同学在2015年共植树多少棵?
某市2011-2015年人均公共绿地面积年增长率统计图 某市2011-2015年人均公共绿地面积统计图

(1)请根据以上信息解答下列问题:
①求2014年该市人均公共绿地面积是多少平方米(精确到0.1)?
②补全条形统计图:
(2)小明同学还了解到自己身边的许多同学都树立起了绿色文明理念,从自身做起,多种树,为提高人均公共绿地面积做贡献,他对所在班级的40多名同学2015年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
| 种树棵数(棵) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 10 | 5 | 6 | 9 | 4 | 6 |
 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为(30+10$\sqrt{3}$)米.(结果保留根号)
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为(30+10$\sqrt{3}$)米.(结果保留根号)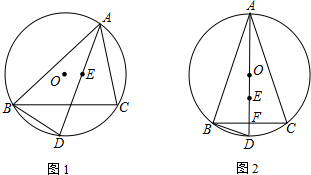

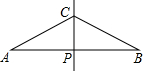 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法: