题目内容
8. 正方形ABCD中,E、F分别为中点,求EG:GH:HC.
正方形ABCD中,E、F分别为中点,求EG:GH:HC.
分析 只需求出EG、GH、HC三条线段分别是线段EC的几分之几即可,注意到正方形对边相互平行,即AB∥CD,延长DF与AB交于点M,由平行线分线段成比例(或相似比)不难得出结论.
解答 解:如图,延长DF、AB交于点M,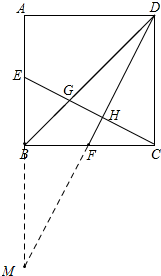
∵ABCD是正方形,
∴AB=BC=CD=AD,AB∥CD,
∴$\frac{EG}{GC}=\frac{BE}{CD}$,$\frac{EH}{HC}=\frac{EM}{CD}$,$\frac{BM}{CD}=\frac{BF}{FC}$
∵E、F分别为AB、BC的中点,
∴BE=AE=$\frac{1}{2}$AB,BF=FC=$\frac{1}{2}$BC,
∴BM=CD=2BE,$\frac{EG}{GC}=\frac{1}{2}$,$\frac{EH}{HC}=\frac{3}{2}$,
∴EG=$\frac{1}{3}$EC,EH=$\frac{3}{5}$EC,
∴GH=$\frac{4}{15}$EC,HC=$\frac{2}{5}$EC,
∴EG:GH:HC=5:4:6.
点评 本题主要考查正方形的基本性质、平行线分线段成比例、相似三角形的判定与性质,属于中档题.利用平行线段分线段成比例将EG、GH、HC分别用EC表示出来是解答问题的关键.

练习册系列答案
相关题目
19. 九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.
九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.
训练后篮球定点定时投篮进球数统计表
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮平均每个人的进球数为5个;
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试数据,训练后篮球定时定点人均进球数比训练之前人均进球数增加25%,请求出训练之前的人均进球数;
(4)根据该统计数据,对于同学们课外活动时间参加体育锻炼有何看法或建议?
 九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.
九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.训练后篮球定点定时投篮进球数统计表
| 进球(个数) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定时定点投篮平均每个人的进球数为5个;
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试数据,训练后篮球定时定点人均进球数比训练之前人均进球数增加25%,请求出训练之前的人均进球数;
(4)根据该统计数据,对于同学们课外活动时间参加体育锻炼有何看法或建议?
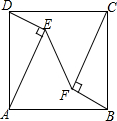 如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.
如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.
 如图,三张正方形纸片,面积分别为13cm2,29cm2和34cm2,将它们拼放在一起,中间恰好围成△ABC,求△ABC的面积.
如图,三张正方形纸片,面积分别为13cm2,29cm2和34cm2,将它们拼放在一起,中间恰好围成△ABC,求△ABC的面积. 在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD.
在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD. 两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC. 如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC. 如图,AB是⊙O的弦,D为⊙O上不与A、B重合的一点,DC⊥AB于点C,$\widehat{AM}$=$\widehat{BM}$,连结DM,求证:∠CDM=∠ODM.
如图,AB是⊙O的弦,D为⊙O上不与A、B重合的一点,DC⊥AB于点C,$\widehat{AM}$=$\widehat{BM}$,连结DM,求证:∠CDM=∠ODM.