题目内容
如图，已知抛物线y=a（x+1）（x-3）（a＞0）与x轴交于A、B两点（A点在B点左侧），与y轴交于C点．
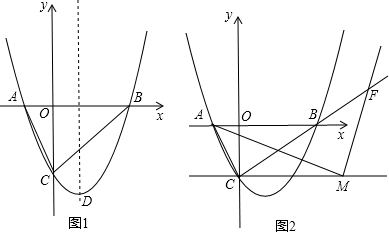
（1）若将直线y=kx向下平移3个单位长度后，直线恰好经过B、C两点，求抛物线的解析式；
（2）在（1）的条件下，若P、Q两点在图1抛物线对称轴上（P点在Q点上方），且∠PAQ=∠ACB，请求出其中符合条件的一组P，Q的坐标；
（3）当AC⊥BC时，
①求a的值；
②如图2过C点作x轴平行线，若M点为该平行线上C点右侧一动点，做AM⊥MF，MF与CB或其延长线相交于F点，试判断
是否为定值？若是请求出该值，若不是请说明理由．
（1）若将直线y=kx向下平移3个单位长度后，直线恰好经过B、C两点，求抛物线的解析式；
（2）在（1）的条件下，若P、Q两点在图1抛物线对称轴上（P点在Q点上方），且∠PAQ=∠ACB，请求出其中符合条件的一组P，Q的坐标；
（3）当AC⊥BC时，
①求a的值；
②如图2过C点作x轴平行线，若M点为该平行线上C点右侧一动点，做AM⊥MF，MF与CB或其延长线相交于F点，试判断
| MF |
| AM |
考点：二次函数综合题
专题：
分析：（1）直线y=kx向下平移3个单位长度后经过BC，则C点向上平移3个单位应为y=kx与y轴的交点（0，0），所以C点为（0，-3）．将C点代入y=a（x+1）（x-3），即可求出a的值，则抛物线解析式可得．
（2）由∠C=∠ACO+∠OCB，所以在A点处构造2个分别等于∠ACO和∠OCB的角即可．如过A做∠PAO=∠ACO，∠QAO=∠OCB，此时记PQ与x轴的交点为N，则有△APN∽△CAO，△ANQ∽△COB．因为已知抛物线的解析式，则A、B、C、N点易求，由边成比例即可得PN，QN，则P、Q点坐标易求．
（3）①对y=a（x+1）（x-3），发现当x=-1和x=3时，y的值都为0，即无论a为何值，抛物线必过A（-1，0），B（3，0）．由AC⊥BC，AB⊥OC，易得三角形相似，则可通过比例得到OC边长，即得C点坐标．此时同（1），代入可求a．
②讨论
的值，发现AM⊥FM，可以考虑连接AF，则M点必在以AF为直径的圆上．又AC⊥BC，若△ACB∽△FAM，则
比为定值，且可根据△ACB求得．观察图2，在圆中等弧对等角，发现∠BAC所对弧为弧NMC，∠AFM所对弧为弧ACM．而弧NMC=劣弧NM+劣弧CM，弧ACM=劣弧AC+劣弧CM，且劣弧NM，劣弧AC同为平行弦AN，CM截圆的弧，即相等，所以角相等，相似成立，进而可求比例定值．
（2）由∠C=∠ACO+∠OCB，所以在A点处构造2个分别等于∠ACO和∠OCB的角即可．如过A做∠PAO=∠ACO，∠QAO=∠OCB，此时记PQ与x轴的交点为N，则有△APN∽△CAO，△ANQ∽△COB．因为已知抛物线的解析式，则A、B、C、N点易求，由边成比例即可得PN，QN，则P、Q点坐标易求．
（3）①对y=a（x+1）（x-3），发现当x=-1和x=3时，y的值都为0，即无论a为何值，抛物线必过A（-1，0），B（3，0）．由AC⊥BC，AB⊥OC，易得三角形相似，则可通过比例得到OC边长，即得C点坐标．此时同（1），代入可求a．
②讨论
| MF |
| AM |
| MF |
| AM |
解答：解：（1）∵直线y=kx，当x=0时，y=0．
∴直线y=kx过O（0，0）．
∵直线y=kx向下平移3个单位长度后经过BC
∴C点向上平移3个单位为O（0，0）．
∴C点坐标为（0，-3）．
∵y=a（x+1）（x-3）过C（0，-3），
∴-3=a（0+1）（0-3），
解得a=1．
整理得，抛物线的解析式为y=x2-2x-3．
（2）如图1，过A做∠PAO=∠ACO，∠QAO=∠OCB，此时∠PAQ=∠ACB，记PQ与x轴的交点为N．
∵抛物线的解析式为y=x2-2x-3，
∴A（-1，0），B（3，0），C（0，-3），PQ在x=1上，N（1，0）．
在△APN和△CAO中，
，
∴△APN∽△CAO．
同理，△ANQ∽△COB．
∴
=
，
=
．
∵AN=2，AO=1，CO=3，OB=3，
∴PN=
，NQ=2．
∴P点坐标为（1，
），Q点坐标（1，-2）．
（3）①∵对抛物线y=a（x+1）（x-3），当x=-1时，y=0，当x=3时，y=0．
∴抛物线y=a（x+1）（x-3）必过A（-1，0），B（3，0），
∴AO=1，OB=3．
∵∠ACB-90°，
∴∠ABC+∠BAC=90°．
∵∠BOC=90°．
∴∠ABC+∠OCB=90°，
∴∠OAC=∠OCB．
在△AOC和△COB中，
，
∴△AOC∽△COB，
∴
=
，
∴CO=
（负值舍去），
∴C点坐标为（0，-
）．
∵y=a（x+1）（x-3）过C（0，-
），
∴-
=a（0+1）（0-3），
解得，a=
．
②
为定值，理由如下：
如图2，连接AF，以AF为直径作圆，由AC⊥BC，AM⊥MF，此时C，M都在圆上．
∵AN∥CM，
∴
=
，
∴
+
=
+
，
∴
=
，
∴∠AFM=∠BAC．
在△AFM和△BAC中，
，
∴△AFM∽△BAC，
∴
=
．
在Rt△AOC和Rt△OBC中
∵AO=1，OC=
，OB=3，
∴AC=2，BC=2
，
∴
=
=
．
∴直线y=kx过O（0，0）．
∵直线y=kx向下平移3个单位长度后经过BC
∴C点向上平移3个单位为O（0，0）．
∴C点坐标为（0，-3）．
∵y=a（x+1）（x-3）过C（0，-3），
∴-3=a（0+1）（0-3），
解得a=1．
整理得，抛物线的解析式为y=x2-2x-3．
（2）如图1，过A做∠PAO=∠ACO，∠QAO=∠OCB，此时∠PAQ=∠ACB，记PQ与x轴的交点为N．
∵抛物线的解析式为y=x2-2x-3，
∴A（-1，0），B（3，0），C（0，-3），PQ在x=1上，N（1，0）．
在△APN和△CAO中，
|
∴△APN∽△CAO．
同理，△ANQ∽△COB．
∴
| PN |
| AN |
| AO |
| CO |
| NQ |
| AN |
| OB |
| CO |
∵AN=2，AO=1，CO=3，OB=3，
∴PN=
| 2 |
| 3 |
∴P点坐标为（1，
| 2 |
| 3 |
（3）①∵对抛物线y=a（x+1）（x-3），当x=-1时，y=0，当x=3时，y=0．
∴抛物线y=a（x+1）（x-3）必过A（-1，0），B（3，0），
∴AO=1，OB=3．
∵∠ACB-90°，
∴∠ABC+∠BAC=90°．
∵∠BOC=90°．
∴∠ABC+∠OCB=90°，
∴∠OAC=∠OCB．
在△AOC和△COB中，
|
∴△AOC∽△COB，
∴
| AO |
| OC |
| CO |
| OB |
∴CO=
| 3 |
∴C点坐标为（0，-
| 3 |
∵y=a（x+1）（x-3）过C（0，-
| 3 |
∴-
| 3 |
解得，a=
| ||
| 3 |
②
| MF |
| AM |
如图2，连接AF，以AF为直径作圆，由AC⊥BC，AM⊥MF，此时C，M都在圆上．
∵AN∥CM，
∴
 |
| AC |
|
| NM |
∴
|
| AC |
|
| CM |
|
| NM |
|
| CM |
∴
|
| ACM |
|
| NMC |
∴∠AFM=∠BAC．
在△AFM和△BAC中，
|
∴△AFM∽△BAC，
∴
| MF |
| AM |
| CA |
| BC |
在Rt△AOC和Rt△OBC中
∵AO=1，OC=
| 3 |
∴AC=2，BC=2
| 3 |
∴
| MF |
| AM |
| 2 | ||
2
|
| ||
| 3 |
点评：本题考查了点平移及函数图象上点的性质，对特殊函数求其是否过定点及定点坐标是常规考点．对（2）、（3）问还要结合二次函数图象性质、三角形相似、圆周角等知识，是一道综合性很强的题目．
练习册系列答案
相关题目
如图所示，在直角坐标系中，点E从O点出发，以1个单位/秒的速度沿x轴正方向运动，点F从O点出发，以2个单位/秒的速度沿y轴正方向运动，B（4，2），以BE为直径作⊙O1．
如图，点P在y轴上，⊙P交x轴于A、B两点，连结BP并延长交⊙P于C，过点C的直线y=2x+b交x轴于D，且⊙P的半径为
在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F． 
如图，已知二次函数y=ax2+bx+3经过A（-1，0）、B（3，0）、C三点，P（2，m）是抛物线与直线l：y=k（x+1）的一个交点．