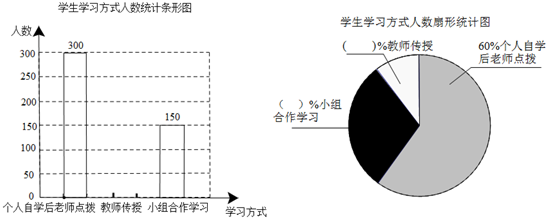
题目内容
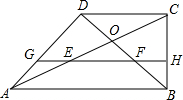 在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F. (1)求证:△FOE≌△DOC;
(2)求tan∠BOC的值;
(3)设△AGE,△EFO,△BFH的面积分别为S1,S2,S3,求S1:S2:S3 的值.
考点:相似三角形的判定与性质,三角形中位线定理,直角梯形
专题:
分析:(1)根据三角形中位线的性质,可得EF与AB的关系,根据ASA,可得证明的结论;
(2)根据正方形的判定与性质,可得DK=BC,根据平行线的性质,可得∠ADC的度数,根据根据角的和差,可得∠ADO的度数,再根据相似三角形的判定与性质,可得DO与BO的关系,根据等角的正切相等,可得答案;
(3)根据相似三角形的判定与性质,可得△AGE∽△ADE,△BFH∽△BDC,S△AGE与S△ADC的关系,S△BFH与S△ADC的关系,根据等底,高是
的两个三角形,可得S△EOF与S△ADC的关系,根据面积的比,可得答案.
(2)根据正方形的判定与性质,可得DK=BC,根据平行线的性质,可得∠ADC的度数,根据根据角的和差,可得∠ADO的度数,再根据相似三角形的判定与性质,可得DO与BO的关系,根据等角的正切相等,可得答案;
(3)根据相似三角形的判定与性质,可得△AGE∽△ADE,△BFH∽△BDC,S△AGE与S△ADC的关系,S△BFH与S△ADC的关系,根据等底,高是
| 1 |
| 3 |
解答:(1)证明:∵EF是△OAB的中位线,
∴EF∥AB,EF=
AB,
∵AB∥CD,AB=2CD,
∴CD∥AB,CD=
AB,
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
在△FOE和△DOC中,
∴△FOE≌△DOC(ASA);
(2)如图:过点D作DK⊥AB,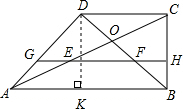
∴BCDK是正方形,
DK=BC,BK=DC=
AB=AK,
∴∠DAB=45°,
∵CD∥AB,
∴∠ADC=135°
∵BC=CD,∠BCD=90°
∴∠BDC=45°
∴∠ADO=90°,
∵CD∥AB,
∴△DOC∽△BOA
∴
=
=
,
设DO=a,BO=2a,
∴AD=BD=3a
∴tan∠BOC=tan∠AOD=3;
(3)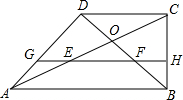 ∵△FOE≌△DOC,
∵△FOE≌△DOC,
∴EO=OC,FO=OD,
线段OA,OB的中点分别为E,F
AE=
AC,FB=
BD,
∵EF∥AB∥CD
∴△AGE∽△ADE,△BFH∽△BDC,
∴
=
,
=
,
∴
=
,
=
,
∵△ADC与△BDC等底等高
∴S△ADC=S△BDC
∴S△AGE=S△BFH
△DOC与△ADC等底,高是
,
∴S△EOF=S△DOC=
S△ADC
∴S1:S2:S3= 1:3:1.
∴EF∥AB,EF=
| 1 |
| 2 |
∵AB∥CD,AB=2CD,
∴CD∥AB,CD=
| 1 |
| 2 |
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
在△FOE和△DOC中,
|
∴△FOE≌△DOC(ASA);
(2)如图:过点D作DK⊥AB,

∴BCDK是正方形,
DK=BC,BK=DC=
| 1 |
| 2 |
∴∠DAB=45°,
∵CD∥AB,
∴∠ADC=135°
∵BC=CD,∠BCD=90°
∴∠BDC=45°
∴∠ADO=90°,
∵CD∥AB,
∴△DOC∽△BOA
∴
| DO |
| BO |
| DC |
| AB |
| 1 |
| 2 |
设DO=a,BO=2a,
∴AD=BD=3a
∴tan∠BOC=tan∠AOD=3;
(3)
 ∵△FOE≌△DOC,
∵△FOE≌△DOC,∴EO=OC,FO=OD,
线段OA,OB的中点分别为E,F
AE=
| 1 |
| 3 |
| 1 |
| 3 |
∵EF∥AB∥CD
∴△AGE∽△ADE,△BFH∽△BDC,
∴
| AE |
| AC |
| 1 |
| 3 |
| BF |
| BD |
| 1 |
| 3 |
∴
| S△AGE |
| S△ADC |
| 1 |
| 9 |
| S△BFH |
| S△BCD |
| 1 |
| 9 |
∵△ADC与△BDC等底等高
∴S△ADC=S△BDC
∴S△AGE=S△BFH
△DOC与△ADC等底,高是
| 1 |
| 3 |
∴S△EOF=S△DOC=
| 1 |
| 3 |
∴S1:S2:S3= 1:3:1.
点评:本题考查了相似三角形的判定与性质,利用了相似三角形的判定与性质,等角的正切值相等,等底等高的三角形的面积相等,稍有点难度.

练习册系列答案
相关题目
 在平面直角坐标系中,O为坐标原点,已知点F(2
在平面直角坐标系中,O为坐标原点,已知点F(2 如图,在平面直角坐标系中,以点M(
如图,在平面直角坐标系中,以点M(
 在平面直角坐标系xOy中,二次函数y=mx2-(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
在平面直角坐标系xOy中,二次函数y=mx2-(m+n)x+n(m<0)的图象与y轴正半轴交于A点.