题目内容
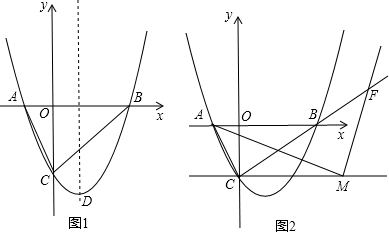
 如图,已知二次函数y=ax2+bx+3经过A(-1,0)、B(3,0)、C三点,P(2,m)是抛物线与直线l:y=k(x+1)的一个交点.
如图,已知二次函数y=ax2+bx+3经过A(-1,0)、B(3,0)、C三点,P(2,m)是抛物线与直线l:y=k(x+1)的一个交点.(1)求二次函数关系式和点C的坐标;
(2)对于动点Q(1,n),求QB-QP的最大值;
(3)若动点M在直线l:y=k(x+1)上方的抛物线上运动,过点M作x轴的垂线交x轴于点F,如果直线AP把线段MF分成1:2的两部分,求点M的坐标.
考点:二次函数综合题
专题:
分析:(1)直接把A(-1,0)、B(3,0)代入二次函数y=ax2+bx+3,求出a、b的值,进而得出二次函数的解析式,再令x=0求出y的值即可得出点C的坐标;
(2)由题意可知动点(1,n)在二次函数的对称轴上,故当点Q、P、B三点共线时,QB-QP的值最大,最大值为QB-QP=PB,把x=2代入y=-x2+2x+3可求出y的值,进而得出P点坐标,再根据两点间的距离公式即可得出结论;
(3)把P(2,3),代入直线y=k(x+1)得,k=1,故可得出直线l的关系式为y=x+1,再根据AP把线段MF分成1:2两部分,可得出
=
或
=
,
设点M的横坐标为x,代入代数式进行计算即可.
(2)由题意可知动点(1,n)在二次函数的对称轴上,故当点Q、P、B三点共线时,QB-QP的值最大,最大值为QB-QP=PB,把x=2代入y=-x2+2x+3可求出y的值,进而得出P点坐标,再根据两点间的距离公式即可得出结论;
(3)把P(2,3),代入直线y=k(x+1)得,k=1,故可得出直线l的关系式为y=x+1,再根据AP把线段MF分成1:2两部分,可得出
| EF |
| MF |
| 1 |
| 3 |
| EF |
| MF |
| 2 |
| 3 |
设点M的横坐标为x,代入代数式进行计算即可.
解答: 解:(1)∵二次函数y=ax2+bx+3经过A(-1,0)、B(3,0),
解:(1)∵二次函数y=ax2+bx+3经过A(-1,0)、B(3,0),
∴
,解得
,
∴二次函数的解析式为:y=-x2+2x+3,D(0,3);
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴动点(1,n)在二次函数的对称轴上,
∴当点Q、P、B三点共线时,QB-QP的值最大,最大值为QB-QP=PB,
把x=2代入y=-x2+2x+3得,y=3,即点P的坐标为(2,3),
∵B(3,0),
∴QB-QP=PB=
=
;
(3)∵把P(2,3),代入直线y=k(x+1)得,k=1,
∴直线l的关系式为y=x+1,
∵AP把线段MF分成1:2两部分,
∴
=
或
=
,
∵∠PAB=45°,
∴EF=AF,
设点M的横坐标为x,则
=
或
=
,解得x=0或x=
,代入y=x+1得,y=3或y=
∴点M的坐标为(0,3),(
,
).
 解:(1)∵二次函数y=ax2+bx+3经过A(-1,0)、B(3,0),
解:(1)∵二次函数y=ax2+bx+3经过A(-1,0)、B(3,0),∴
|
|
∴二次函数的解析式为:y=-x2+2x+3,D(0,3);
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴动点(1,n)在二次函数的对称轴上,
∴当点Q、P、B三点共线时,QB-QP的值最大,最大值为QB-QP=PB,
把x=2代入y=-x2+2x+3得,y=3,即点P的坐标为(2,3),
∵B(3,0),
∴QB-QP=PB=
| 12+32 |
| 10 |
(3)∵把P(2,3),代入直线y=k(x+1)得,k=1,
∴直线l的关系式为y=x+1,
∵AP把线段MF分成1:2两部分,
∴
| EF |
| MF |
| 1 |
| 3 |
| EF |
| MF |
| 2 |
| 3 |
∵∠PAB=45°,
∴EF=AF,
设点M的横坐标为x,则
| x+1 |
| -(x+1)(x-3) |
| 1 |
| 3 |
| x+1 |
| -(x+1)(x-3) |
| 2 |
| 3 |
| 3 |
| 2 |
| 15 |
| 4 |
∴点M的坐标为(0,3),(
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、最值问题等知识,难度适中.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
设x1、x2是一元二次方程x2+4x-3=0的两个根,2x1(x22+5x2-3)+a=2,则a的值为( )
| A、-2 | B、4 | C、8 | D、10 |
我国以2011年11月1日零时为标准时点进行了第六次全国人口普查,普查得到全国总人口为1370536875人,该数用科学记数法表示并保留三位有效数字为( )
| A、1.37×109 |
| B、13.7×108 |
| C、1.4×109 |
| D、13.7 亿 |
 如图,已知△ABC中,延长AC边上的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF,AG.
如图,已知△ABC中,延长AC边上的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF,AG.