题目内容
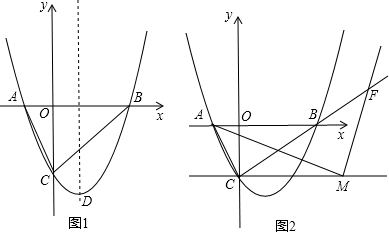
 如图所示,在直角坐标系中,点E从O点出发,以1个单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒的速度沿y轴正方向运动,B(4,2),以BE为直径作⊙O1.
如图所示,在直角坐标系中,点E从O点出发,以1个单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒的速度沿y轴正方向运动,B(4,2),以BE为直径作⊙O1.(1)若点E、F同时出发,设线段EF与线段OB交于点G,试判断点G与⊙O1的位置关系,并证明你的结论;
(2)在(1)的条件下,连结FB,几秒时FB与⊙O1相切?
考点:直线与圆的位置关系,坐标与图形性质,点与圆的位置关系
专题:动点型
分析:(1)要判断点G与⊙O1的位置关系,只需比较O1G与⊙O1的半径O1B的大小;
(2)如果t秒时FB与⊙O1相切,那么∠FBE=90°;在RT△BEF与RT△OEF中,根据EF不变列出方程,求出t的值.
(2)如果t秒时FB与⊙O1相切,那么∠FBE=90°;在RT△BEF与RT△OEF中,根据EF不变列出方程,求出t的值.
解答:解:(1)∵点B的坐标为(4,2),
又∵OE:OF=1:2,∠OFE=∠EOB.
∴∠FGO=90°,
又∵BE为⊙O1的直径,
∴点G在⊙O1上.
(2)过点B作BM⊥OF,设
OE=x,则OF=2x,
BF2=BM2+FM2=42+(2x-2)2=4x2-8x+20,BE2=(4-x)2+22=x2-8x+20,
又∵OE2+OF2=BE2+BF2,
∴x2+4x2=5x2-16x+40,
∴x=
(x>0),
即
秒时,BF与⊙O1相切.
又∵OE:OF=1:2,∠OFE=∠EOB.
∴∠FGO=90°,
又∵BE为⊙O1的直径,
∴点G在⊙O1上.
(2)过点B作BM⊥OF,设
OE=x,则OF=2x,
BF2=BM2+FM2=42+(2x-2)2=4x2-8x+20,BE2=(4-x)2+22=x2-8x+20,
又∵OE2+OF2=BE2+BF2,
∴x2+4x2=5x2-16x+40,
∴x=
| 5 |
| 2 |
即
| 5 |
| 2 |
点评:本题综合考查了切线的判定,三角函数等知识,解题中要善于抓住不变量,找到等量关系,题目有一定难度,可以考查学生的综合实力.

练习册系列答案
相关题目
设x1、x2是一元二次方程x2+4x-3=0的两个根,2x1(x22+5x2-3)+a=2,则a的值为( )
| A、-2 | B、4 | C、8 | D、10 |
 如图,在锐角△ABC中,探究
如图,在锐角△ABC中,探究 如图:点A、B、C在⊙O上,∠AOC=120°,则∠ABC的度数是
如图:点A、B、C在⊙O上,∠AOC=120°,则∠ABC的度数是
 在平面直角坐标系中,O为坐标原点,已知点F(2
在平面直角坐标系中,O为坐标原点,已知点F(2