题目内容
若a=
,b=
,求
-(
-
)÷
.
| 1 | ||
|
| 1 | ||
|
a+2
| ||
| a-b |
| ||
a+
|
| ||
b-
|
| ||
b+
|
考点:二次根式的化简求值
专题:
分析:首先化简a=
+1,b=
-1,那么ab=(
+1)(
-1)=1,a+b=2
,a-b=2,然后根据二次根式的性质及运算法则进行化简计算即可.
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:∵a=
=
+1,b=
=
-1,
∴ab=(
+1)(
-1)=1,a+b=2
,a-b=2,
∴
-(
-
)÷
=
-(
-
)•
=
+1-
+
=
+1-
+
=
+1-(
-1)+(-1)
=1.
| 1 | ||
|
| 2 |
| 1 | ||
|
| 2 |
∴ab=(
| 2 |
| 2 |
| 2 |
∴
a+2
| ||
| a-b |
| ||
a+
|
| ||
b-
|
| ||
b+
|
=
2
| ||
| 2 |
| ||
| a+1 |
| ||
| b-1 |
| b+1 | ||
|
=
| 2 |
| b+1 |
| a+1 |
| b+1 |
| a(b-1) |
=
| 2 |
| ||
|
| ||||
(
|
=
| 2 |
| 2 |
=1.
点评:本题考查了二次根式的化简求值,熟练掌握二次根式的性质及运算法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程
+
+
+
+
=18的解是( )
| x-2 |
| 3 |
| x-3 |
| 5 |
| x-2 |
| 7 |
| x-5 |
| 9 |
| x-1 |
| 11 |
| A、x=-32 | B、x=32 |
| C、x=-23 | D、x=23 |
若
+1-4b+4b2=0,则a2+
+b的值为( )
| a2-4a+4 |
| 1 |
| a |
| A、4 | B、5.5 | C、4.5 | D、5 |
 如图中,若BD、CD为角平分线,且∠A=50°,∠E=130°,∠则∠D=
如图中,若BD、CD为角平分线,且∠A=50°,∠E=130°,∠则∠D=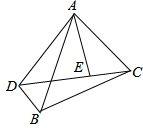 如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.
如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.