题目内容
 如图中,若BD、CD为角平分线,且∠A=50°,∠E=130°,∠则∠D=
如图中,若BD、CD为角平分线,且∠A=50°,∠E=130°,∠则∠D=考点:三角形内角和定理
专题:
分析:连接BC,根据三角形内角和定理求出∠EBC+∠EC=50°,∠ABC+∠ACB=130°,求出∠ABE+∠ACE=80°,根据角平分线定义得出∠DBE=
∠DCE=
∠ACE,求出∠DBE+∠DCE=
(∠ABE+∠ACE)=40°,根据三角形内角和定理求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:
连接BC,
∵∠E=130°,∠A=50°,
∴∠EBC+∠ECB=180°-130°=50°,∠ABC+∠ACB=180°-50°=130°,
∴∠ABE+∠ACE=130°-50°=80°,
∵BD、CD为角平分线,
∴∠DBE=
∠DCE=
∠ACE,
∴∠DBE+∠DCE=
(∠ABE+∠ACE)=40°,
∴∠D=180°-(∠DBC+∠DCB)=180°-(∠DBE+∠DCE)-(∠EBC+∠ECB)=180°-(40°+50°)=90°,
故答案为:90.

连接BC,
∵∠E=130°,∠A=50°,
∴∠EBC+∠ECB=180°-130°=50°,∠ABC+∠ACB=180°-50°=130°,
∴∠ABE+∠ACE=130°-50°=80°,
∵BD、CD为角平分线,
∴∠DBE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBE+∠DCE=
| 1 |
| 2 |
∴∠D=180°-(∠DBC+∠DCB)=180°-(∠DBE+∠DCE)-(∠EBC+∠ECB)=180°-(40°+50°)=90°,
故答案为:90.
点评:本题考查了对三角形内角和定理和角平分线定义的应用,注意:三角形的内角和等于180°.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
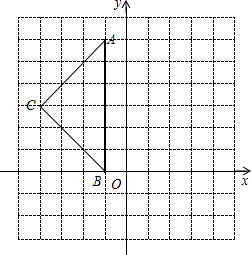 如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).
如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).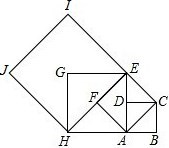 如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….
如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….