题目内容
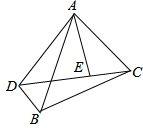 如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.
如图,△ADE与△ABC有公共顶点A,∠BAD=∠CAE.(1)请你写一个适当的条件,使△ADE∽△ABC,则需添加的条件可以是
(2)由(1)能否得出其他的相似三角形?如果能,请说明理由.
考点:相似三角形的判定
专题:
分析:(1)利用两角对应相等的三角形相似进而得出即可;
(2)利用相似三角形的性质得出
=
,进而求出即可.
(2)利用相似三角形的性质得出
| AB |
| AD |
| AC |
| AE |
解答:解:(1)使△ADE∽△ABC,则需添加的条件可以是:∠ADC=∠ABC或∠AED=∠ACB,
理由:∵∠BAD=∠CAE,
∴∠BAD+∠BAE=∠BAE+∠CAE,
即∠DAE=∠CAB,
又∵∠ADC=∠ABC,
∴△ADE∽△ABC,
故答案为:∠ADC=∠ABC或∠AED=∠ACB;
(2)△ABD∽△ACE.
理由:∵△ADE∽△ABC,∠BAC=∠DAE,
∴
=
,∠BAC-∠DAC=∠DAE-∠CAE,
∴
=
,∠BAD=∠CAE,
∴△ABD∽△ACE.
理由:∵∠BAD=∠CAE,
∴∠BAD+∠BAE=∠BAE+∠CAE,
即∠DAE=∠CAB,
又∵∠ADC=∠ABC,
∴△ADE∽△ABC,
故答案为:∠ADC=∠ABC或∠AED=∠ACB;
(2)△ABD∽△ACE.
理由:∵△ADE∽△ABC,∠BAC=∠DAE,
∴
| AB |
| AD |
| AC |
| AE |
∴
| AB |
| AC |
| AD |
| AE |
∴△ABD∽△ACE.
点评:此题主要考查了相似三角形的判定与性质,熟练应用相似三角形的性质是解题关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,已知FD⊥BC于D,DE⊥AB于E,∠B=∠C,∠AFD=140°,求∠EDF的度数.
如图,已知FD⊥BC于D,DE⊥AB于E,∠B=∠C,∠AFD=140°,求∠EDF的度数.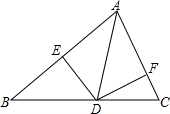 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是