题目内容
18.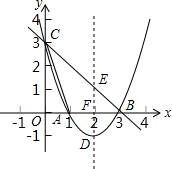 在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=-x沿y轴向上平移3个单位长度后恰好经过B,C两点.
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=-x沿y轴向上平移3个单位长度后恰好经过B,C两点.(1)求抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连结CD,求∠OCA与∠OCD两角和的度数.
分析 (1)根据平移的规律,可得BC的解析式,根据自变量与函数值的对应关系,可得B、C点坐标,根据待定系数法,可得BC的解析式;
(2)根据自变量与函数值的对应关系,可得A、B、C点坐标,根据配方法,可得D点坐标,根据等腰三角形的性质,可得BC的长,根据相似三角形的判定与性质,可得PF的长,根据线段的和差,可得F点坐标;
(3)根据轴对称,可得A′点,根据勾股定理,可得A′C,A′D,根据勾股定理的逆定理,可得∠CA′D=90°,根据等量代换,可得答案.
解答 解:(1)直线y=-x沿y轴向上平移3个单位长度后经过y轴上的点C,得
y=-x+3,即C(0,3),(3,0).
抛物线y=x2+bx+c过点B,C,
$\left\{\begin{array}{l}{9+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$.
故抛物线的解析式为y=x2-4x+3.
(2)由y=x2-4x+3,当y=0时,x2-4x+3=0,解得x=1,x=3,即A(1,0),B(3,0).
y=x2-4x+3=(x-2)2-1,D(2,-1).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形.
∴∠OBC=45°,CB=3$\sqrt{2}$.
如图1,设抛物线对称轴与x轴交于点F,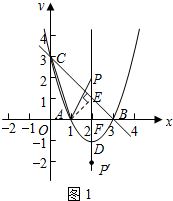
AF=$\frac{1}{2}$AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90°.
可得BE=AE=$\sqrt{2}$,CE=2$\sqrt{2}$.
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴$\frac{AE}{AF}$=$\frac{CE}{PF}$,$\frac{\sqrt{2}}{1}$=$\frac{2\sqrt{2}}{PF}$.
解得PF=2.
点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,-2).
(3)如图2,作点A(1,0)关于y轴的对称点A′,则A′(-1,0). 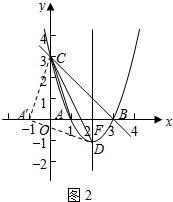
连结A′C,A′D,
可得A′C=AC=$\sqrt{10}$,∠OCA′=∠OCA.
由勾股定理可得CD2=20,A′D2=10.
又∵A′C2=10,
∴A′D2+A′C2=CD2.
∴△A′DC是等腰直角三角形,∠CA′D=90°,
∴∠DCA′=45°.
∴∠OCA′+∠OCD=45°.
∴∠OCA+∠OCD=45°.
即∠OCA与∠OCD两角和的度数为45°.
点评 本题考查了二次函数综合题,利用自变量与函数值的对应关系得出B、C点坐标是解题关键;利用相似三角形的判定与性质得出PF的长是解题关键;利用勾股定理的逆定理得出∠CA′D=90°是解题关键.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案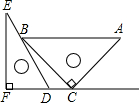 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )| A. | 25° | B. | 20° | C. | 15° | D. | 18° |
| A. | m≥4 | B. | m≤4 | C. | 3≤x<4 | D. | 3<x≤4 |
| A. | 9.07×10-4 | B. | 9.07×10-6 | C. | 9.07×105 | D. | 9.07×10-5 |
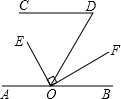 已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.
已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.