题目内容
17.求函数y=x2-2x-3(2≤x≤3)的最值.分析 首先求得抛物线的对称轴为x=1,然后根据a=1>0,可知当2≤x≤3时,y随x的增大而增大,从而可求得函数y=x2-2x-3(2≤x≤3)的最大值和最小值.
解答 解:抛物线的对称轴为x=$-\frac{b}{2z}$=1,
∵a=1>0,
∴当2≤x≤3时,y随x的增大而增大.
∴当x=2时,有最小值,最小值为y=-3,当x=3时,有最大值,最大值为y=0.
点评 本题主要考查的是二次函数的最值,确定出抛物线的对称轴,然后根据二次函数的增减性进行判断是解题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
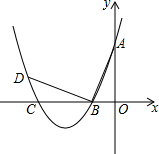 如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
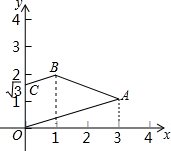 如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.
如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.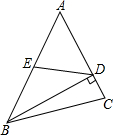 如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.
如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.