Question

16．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、
B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A₁B₁C₁；
（2）以点B为位似中心，在网格内画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且相似比为2：1，点A₂的坐标（-3，2）；
（3）△A₂B₂C₂的面积是10平方单位．

Answer 1

分析 （1）利用点平移的坐标规律，写出A₁、B₁、C₁的坐标，然后即可得到△A₁B₁C₁为所作；
（2）延长BA到A₂，使BA₂=2BA，则点A₂为点A的对应点，同样方法得到C点的对应点C₂，点B₂与B点重合，则可得到△A₂B₂C₂，然后写出点A₂的坐标；
（3）用一个矩形的面积分别减去三个直角三角形的面积可得到△A₂B₂C₂的面积．

解答 解：（1）如图，△A₁B₁C₁为所作；
（2）如图，△A₂B₂C₂为所作，点A₂的坐标为（-3，2）；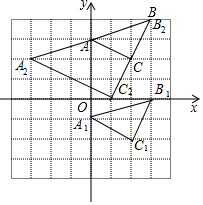

（3）△A₂B₂C₂的面积=6×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×6=10．
故答案为（-3，2），10．

点评 本题考查了作图-位似变化：先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；接着根据位似比，确定能代表所作的位似图形的关键点；然后顺次连接上述各点，得到放大或缩小的图形．