题目内容
12.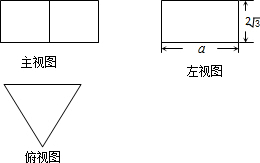 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 观察给出的图形可知,正三棱柱的高是2$\sqrt{3}$,正三棱柱的底面正三角形的高是a,根据三角函数可得底面边长为$\frac{2\sqrt{3}}{3}$a,根据长方形的面积公式和这个正三棱柱的侧面积为8$\sqrt{3}$,可得关于a的方程,解方程即可求得a的值.
解答 解:观察给出的图形可知,正三棱柱的高是2$\sqrt{3}$,正三棱柱的底面正三角形的高是a,则底面边长为$\frac{2\sqrt{3}}{3}$a,
依题意有$\frac{2\sqrt{3}}{3}$a×2$\sqrt{3}$×3=8$\sqrt{3}$,
解得a=$\frac{2}{3}$$\sqrt{3}$.
故选:A.
点评 考查了由三视图判断几何体,关键是由三视图得到正三棱柱的高和底面边长.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
2.-3、0、1、-1四个数中,最小的数是( )
| A. | -3 | B. | 0 | C. | 1 | D. | -1 |
7.在一个三角形中,已知AB=AC=6cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为5cm的圆,则下列说法正确的是( )
| A. | 点A在⊙D外 | B. | 点B在⊙D上 | C. | 点C在⊙D内 | D. | 无法确定 |




 如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68.
如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68.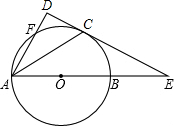 如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.