题目内容
3.“嘀嘀打车”是时下非常流行的打车、租车软件.学校想通过“嘀嘀打车”的专车服务来租用教师和学生的外出用车,已知学校共有6名教师和234名学生集体外出活动,准备租用45座大客车或30座小客车(两种车型可混合租用).已知租车的费用标准如下:若租用1辆大车2辆小车共需租车费1000元;若若租用2辆大车1辆小车共需租车费1100元.(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名教师,且总租车费用不超过2300元,求最省钱的租车方案.
分析 (1)设大车每辆的租车费是x元、小车每辆的租车费是y元.根据题意:“租用1辆大车2辆小车共需租车费1000元”;“租用2辆大车一辆小车共需租车费1100元”;列出方程组,求解即可;
(2)240名师生都有座位,租车总辆数≥6;每辆车上至少要有一名教师,租车总辆数≤6.故租车总数是6辆,设大车辆数是x辆,则租小车(6-x)辆.根据“总座位大于等于240,总费用小于等于2300元”列出不等式组,并解答.
解答 解:(1)设大、小车每辆的租车费各是x、y元.
则$\left\{\begin{array}{l}{x+2y=1000}\\{2x+y=1100}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=400}\\{y=300}\end{array}\right.$.
答:大、小车每辆的租车费各是400元、300元.
(2)240名师生都有座位,租车总辆数≥6;每辆车上至少要有一名教师,租车总辆数≤6.故租车总数是6辆,设大车辆数是x辆,则租小车(6-x)辆
$\left\{\begin{array}{l}{45x+30(6-x)≥240}\\{400x+300(6-x)≤2300}\end{array}\right.$,
解得:4≤x≤5,
∵x是正整数,
∴x=4或5.
于是又两种租车方案,
方案1:大车4辆 小车2辆 总租车费用2200元,
方案2:大车5辆 小车1辆 总租车费用2300元,可见最省钱的是方案1.
点评 本题考查了二元一次方程组的应用,一元一次不等式的应用和理解题意的能力,关键是根据题目所提供的等量关系和不等量关系,列出方程组和不等式求解.

练习册系列答案
相关题目
13.学校组织的实践活动中,晓华同学用纸板制作了一个圆锥模型,它的底面直径为4,高为2$\sqrt{3}$,则这个圆锥的侧面积是( )
| A. | 8π | B. | 16π | C. | 4$\sqrt{3}$π | D. | 8$\sqrt{7}$π |
14.下列结论正确的是( )
| A. | $-\sqrt{(-6)^{2}}=-6$ | B. | $(-\sqrt{3})^{2}=9$ | C. | $\sqrt{({-16)}^{2}}=±16$ | D. | $-(-\sqrt{\frac{16}{25}})^{2}=\frac{16}{25}$ |
8.$\sqrt{(3.1-\sqrt{10})^{2}}$的值等于( )
| A. | $\sqrt{10}$-3.1 | B. | 3.1±$\sqrt{10}$ | C. | 3.1-$\sqrt{10}$ | D. | ±(3.1-$\sqrt{10}$) |
12.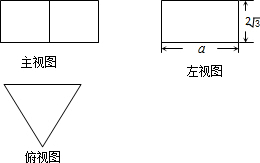 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
4.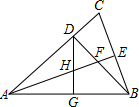 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )| A. | AH=2DF | B. | AF=2HE | C. | AF=2CE | D. | DH=DF |